En mi grupo de amigos había dos bandos. De un lado estaban los soñadores, los que se imaginaban literalmente a bordo de la Enterprise y se dedicaban a especular sobre situaciones imaginarias, involucrando naves espaciales que se alargaban hasta el infinito a medida que su velocidad se acercaba a la de la luz mientras que los relojes del puente de mando se detenían. Del otro estábamos los freakies del CERN, enganchados al Investigación y Ciencia y a todo lo que llegara del laboratorio en Suiza. Puestos a soñar, soñábamos con poder trabajar en aquella Meca donde se juntaban los mejores físicos del mundo. Allá por 1980 me parecía que tenía tantas posibilidades de que me dieran una beca para ir al CERN (España ni siquiera formaba parte del consorcio internacional que gestiona el laboratorio por aquella época) como de viajar a los confines de la galaxia con el capitán Kirk.
De todas las rarezas de la relatividad la que más nos excitaba era la dilatación temporal. Para explicar el fenómeno podemos recurrir a un Gedankenexperiment involucrando —como no—, a nuestros héroes de Star Trek. El experimento es el siguiente. A bordo de la Enterprise Kirk dispara un rayo láser a un blanco que se encuentra situado en el otro extremo del puente de mando, de tal manera que el rayo se mueve en dirección exactamente perpendicular a la del movimiento de la nave. El blanco se encuentra a 4 metros de Kirk. Para calcular el tiempo que le cuesta a la luz viajar hasta el blanco, recordemos que
ahora bien, la velocidad de la luz es c, como ya hemos visto. El espacio que recorre son cuatro metros. Por tanto, el tiempo que invierte la luz en llegar al blanco (de acuerdo con el reloj de a bordo) es:
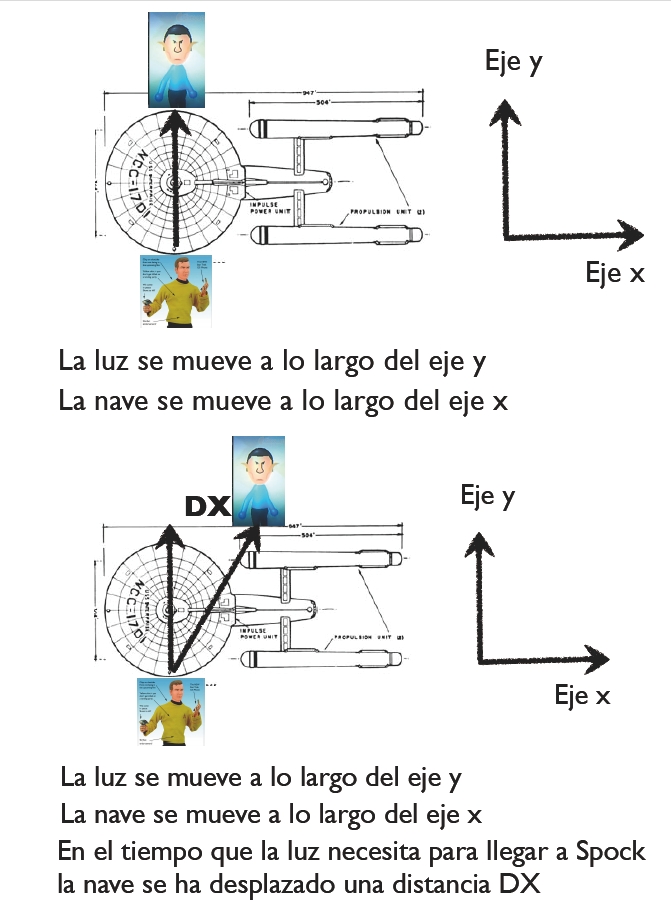
Justo en el preciso momento en que Kirk dispara su rayo, la Enterprise pasa frente a la estación Deep Space nine, donde Mr. Spock observa también el recorrido de la luz (huelga decir que el puente de mando de la Enterprise está hecho de metacristal de litio, perfectamente transparente, de tal manera que Spock puede ver todo lo que ocurre dentro).
Desde el punto de vista de Mr. Spock, mientras el rayo de luz se propaga hacia él —siguiendo la dirección de un imaginario eje al que podemos llamar Y—, la Enterprise se mueve en dirección perpendicular tanto a Mr. Spock como al rayo de luz —por tanto podemos elegir otros dos ejes perpendiculares, X, para desplazar la nave y Z para situar a Mr. Spock—. La consecuencia es que la trayectoria de la luz, desde el punto de vista de Spock, sigue una trayectoria diagonal en el plano X-Y. Puesto que la Enterprise viaja a velocidades próximas a las de la luz nada nos cuesta imaginar que la nave se desplaza (a lo largo de X) 3 metros en el tiempo que le cuesta a la luz viajar (a lo largo de Y) 4 metros. Para obtener la longitud de la trayectoria diagonal que sigue la luz (desde el punto de vista de Spock) basta con aplicar el teorema de Pitágoras:
Donde x es la distancia que viaja la nave a lo largo del eje X (3 metros) e y es la distancia que viaje la luz a lo largo del eje Y (4 metros). Por tanto, la distancia que viaja la luz en el sistema de referencia de Spock es d =√ (9 + 16) = 5 metros. Para calcular el tiempo que ha invertido la luz en el viaje nuestra héroe divide, al igual que hace Kirk a bordo de la Enterprise, la distancia que la luz recorre (5 metros) por la velocidad de la luz, que también es c, ya que la velocidad de la luz es la misma en todos los sistemas de referencia. Es decir:
¿Conclusión? El tiempo que mide Kirk es distinto al tiempo que mide Spock. El cociente entre ambos tiempos es de 4/5, o lo que es lo mismo, el reloj de la Enterprise mide 8 segundos por cada diez segundos medidos en el reloj de la estación en la que se encuentra Spock.
No es que al reloj de la Enterprise le pase nada en especial. Lo que ocurre es que la nave se mueva a una velocidad grande comparada con la de la luz, que por cierto podemos calcular fácilmente. En el sistema de referencia de Spock, la nave avanza 3 metros en el tiempo que la luz avanza 5 metros y por tanto la velocidad de la nave relativa a la velocidad de la luz (una cantidad famosamente conocida como β) es:
Debido a esa velocidad, el tiempo se dilata en la Enterprise. El reloj de a bordo marcha 8 segundos por cada diez en Deep Space nine, pero también los ciclos del ordenador de a bordo (y los ciclos mentales de Kirk) se ralentizan por el mismo factor 0.8. Y también la tripulación de la nave envejece 8 años por cada diez años que pasan para la tripulación de la estación orbital. Por supuesto, ni unos ni otros notan diferencia alguna en su percepción del paso del tiempo.
Esto quiere decir que, para una Enterprise que viaja a una fracción diminuta de la velocidad de la luz, el tiempo se alarga tanto que cada parpadeo de Kirk podría suponer toda una vida de Spock (y más, como veremos en la próxima entrega). La secta de los místicos, aquellos de mis amigos a los que les gustaba darle vueltas y vueltas a estas cosas, se pasaban las noches en blanco imaginando argumentos para novelas de Ciencia Ficción que siempre eran variantes de la misma idea. Kirk viaja a una estrella lejana y, a velocidades próximas a la de la luz, apenas envejece. Pero cuando regresa a casa han pasado 50, o 100, o 1000 años en la Tierra y nuestro héroe es un extraño en su propio mundo. O, dicho de otro modo, los viajes al futuro son posibles, de acuerdo a la teoría de la relatividad. Pero al pasado no se puede volver —o quizá sí, quizá se vuelve como un fantasma translúcido e impotente para cambiar el destino—. Y viajar al futuro es perder el presente. La idea no me hacía gracia ya entonces y todavía me sigue pareciendo terrible.
Recuerdo que cuando fue mi turno de parir un relato imaginé un mundo en el que los criminales eran condenados a viajar a una estrella a cincuenta años luz de la tierra, donde se encontraban las mayores minas —de uranio, torio, litio, el material es lo de menos, a fin de cuentas la idea es vieja, las minas del rey Salomón, cuya última encarnación la hemos vuelto a disfrutar en el Avatar de Cameron—. El viaje de ida y vuelta costaba 10 años en el sistema de referencia del condenado —un viaje del que no se enteraba en todo caso, convenientemente hibernado en los congeladores de a bordo— y la condena transcurría en el planeta-mina, veinte años de trabajos forzados. Pero lo peor era lo que aguardaba a los desdichados Odiseos a su regreso al hogar. Un mundo desconocido, donde todos sus seres queridos habían desaparecido —en mi novela futurista la gente seguía sin vivir más de 100 años—. Al cabo de 130 años nada quedaba de los lugares queridos, ningún superviviente entre amigos y familia. Nada más terrible que regresar a un futuro en el que tus hijos han muerto, tus nietos son ancianos, tus bisnietos jamás han oído hablar de ti. Muchos enloquecían, alguno se suicidaba, la mayoría optaba por regresar al planeta-mina, al gulag que se había convertido en su único hogar. Titulé aquella novela: No volverás a Itaca.



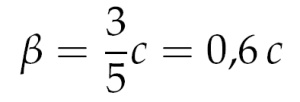






Pingback: Juan José Gómez Cadenas: No volverás a Itaca
Juan José: Entiendo la mitad de la mitad de lo que cuentas, mi cabeza no da para más, pero aún con esa mitad de la mitad lo que leo me parece magnífico. Muchas gracias.
Jolin cuesta de entender para la gente media.
Conocer las más elementales reglas gramaticales y ortográficas ayuda bastante en ese aspecto.
«naves espaciales que se alargaban hasta el infinito a medida que su velocidad se acercaba a la de la luz»
Aquí se cumple aquello de «no permitas que la realidad te estropee un buen efecto gráfico»
A medida que un objeto se acerca a la velocidad de la luz su longitud disminuye (l1 = l0 x sqr( 1-(v²/c²))
Solo veo una pega. La estación Deep Space 9 es de un siglo después de las aventuras del Capitan Kirk. Algo raro tuvo que pasar para que coincidan todos al mismo tiempo ;).
Yo he tenido más suerte y sí he podido entender todos los detalles. Muchísimas gracias, es una explicación excelente.
Vaya que si! La frase deberia haber sido: «Naves que se contraían hasta el infinito» Gracias!
En lo que se refiere al desfase temporal entre Deep Space Nine y las aventuras de Kirk, tendremos que inventar algún truco relativista (ya tenemos unos cuantos) para hacerlos coincidir…
Gracias!
En ningún momento se consiguió demostrar que la teoría de la relatividad de Poincaré fuera falsa, las evidencias estuvieron fortaleciendo una hipótesis que, ahora con los neutrinos superlumínicos en la palestra, necesita una revisión. O, al menos, una revisión tan buena como la que se ha estado aplicando a los propios superneutrinos. Al fin y al cabo, las bolitas que caen en un plano de cuatro dimensiones también es incompatible con la teleportación cuántica, que es un hecho empírico. Considerando que para Einstein medir significaba «poner una regla y comparar», sólo puedo decir que tiene más sentido pensar que nuestros sistemas de medida pueden verse alterados, y que no es lo mismo un cronómetro químico que un cronómetro más mecánico.
Entiendo lo que has explicado y la verdad que es interesante, pero tengo una duda, ¿no seria posible que un cuerpo con masa a la velocidad de la luz deformara el espacio tiempo de tal manera que la ecuación de pitagoras no pudiera aplicarse? debido a que el espacio dentro de la nave esta mas deformado que el espacio de fuera. Quizas sea una tonteria, no lo se.
El espacio tiempo, en efecto, se deforma (de eso da cuenta la teoría general de la relatividad), pero las ecuaciones siguen siendo válidas… la forma en que las deduzco aquí es muy elemental, pero las fómulas (que veremos con más detalle en la próxima entrega) son generales.
Gracias!
Las naves de Star Trek nunca alcanzan velocidades cercanas a las de la luz (de hecho, no pueden superar la velocidad de los impulsores de popa). Se basan en deformar el espacio según la métrica de Alcubierre de forma que los efectos relativistas dentro de la burbuja de curvatura no suceden. Es un efecto similar al que sucede debido a la expansión métrica del espacio que lleva a galaxias hasta los 90.000 millones de años luz de distancia en un universo de apenas 13.700 millones de años.
* Digo velocidad de los impulsores, ya que hay un límite de velocidad sub-curvatura que creo que es impuesto por la Federación, en torno a los 0.5c.
Qué quiero decir, que para hacer la locurilla bien tendríamos que tener en cuenta la deformación en los extremos de la burbuja warp. De hecho, creo que la materia no puede interaccionar con lo que sucede dentro, pero eso ya se me escapa.
Otra cosilla, los efectos de dilación temporal empiezan a ser notables a partir de los 0.83c, ¿no? (que es cuando el tiempo empieza a ir el doble de lento para el objeto observado desde el punto de vista de nuestro marco de referencia) . Y esto ya no es una fracción diminuta, oiga.
Me ha encantado el ejemplo, muy bien explicado! Sin embargo me ha surgido una pequeña duda, seguramente sea una estupidez. Espero a ver si alguien puede sacarme de ella.
En ningún momento se da el valor de ‘c’ que todos, algunos mas y otros menos, sabemos que es del orden de aproximadamente 3×10^8 m/s. Aunque de todas formas al final cuando hacemos el cociente Tk/Ts el resultado es independiente del valor de ‘c’. Lo que da la impresión de que la dilatación del tiempo es la misma que si ‘c’ fuese igual a 1 m/s, pero sabemos que eso no ocurre. Un ejemplo sería si extrapolamos de una nave a un coche y de un pistola láser a una pistola convencional. Solo ocurre cuando la velocidad se acerca a ‘c’. ¿Por qué ocurre esto?
Solo se me ocurre pensar que cuando calculamos la velocidad en el sistema de referencia de Spok el rayo tiene una velocidad (c,c) (ejeX,ejeY) luego su módulo sería c multiplicado por raiz(2). Lo que nos da un número mayor que ‘c’, algo imposible si tomamos como principio que no se puede superar la velocidad la luz. De este modo, el calculo de Ts si que sería 5/c en vez de 5/(c * raiz(2)), que es como debería de ser si no se aplica el principio.
Y efectivamente en el artículo cuando se dice: «Para calcular el tiempo que ha invertido la luz en el viaje nuestra héroe divide, al igual que hace Kirk a bordo de la Enterprise, la distancia que la luz recorre (5 metros) por la velocidad de la luz, que también es c, ya que la velocidad de la luz es la misma en todos los sistemas de referencia.» se deja bien claro que se divide nuevamente entre ‘c’.
No se si me estoy equivocando, la física no es lo mio. Pero en fin, la duda entonces sería ¿por qué es esto solo aplicable cuando ‘c’ es aproximadamente 3×10^8 m/s?
Enhorabuena por el artículo, espero que se entienda lo que quiero decir. Saludos
Si entiendo bien te preguntas si la cuenta seria la misma independientemente del valor preciso de «c». Asi es. Lo que el principio de la relatividad dice es que «c» es la misma en todos los sistemas de referencia. El valor de «c» es un «porque si», la naturaleza ha escogido que la velocidad de la luz en el vacio sea esa y no otra.
Que cruel la novela. xD
Pingback: Enero | Pero ahora quiero ser pequeño!
Debo ser muy listo o muy tonto, porque esto del rayo de Einstein no lo entiendo ni lo entenderé nunca. Yo habría puesto el dibujo con un mismo eje Y en la página, y que la nave se mueva hacia la izquierda. Tendríamos la nave dibujada arriba con el rayo que se lanza de abajo a arriba (eje Y), y la nave dibujada abajo DESPLAZADA HACIA LA IZQUIERDA RESPECTO DE LA DE ARRIBA.
Entonces en el dibujo de abajo el rayo impactaría a la derecha de Kirk, recorriendo una diagonal, mientras que para Spock el rayo recorrería una recta sobre el eje Y (recordemos, eje inmóvil).
El rayo dentro de la nave debería «quedarse atrás» y no impactar en el punto «justo enfrente» de donde se dispara, sino a la derecha (la nave se mueve hacia la izquierda). Saldría de la nave a la altura de la letra N de NCC en el dibujo.
Para Spock, que está quieto, el rayo va de frente de forma normal.
Ya se que no es así, pero debería.
Este es mi punto de vista:
http://www.flickr.com/photos/74721593@N07/6735490605/in/photostream
Para B, el fotón se mueve a más de c.
Debería ser así. Es lo lógico. Jeje.
Por favor, no escribas «más sencillo». El que quiera comprender que le de al seso, no es tan difícil, lo que pasa es que si uno no está acostumbrado, leer una descripción espacial de trayectorias es complicado, pero los que estén interesados con un papel y un lápiz en 30 segundos habrán resuelto sus dudas siguiendo la descripción.
Para mí la clave de este artículo (o fascículo) es el: «Por supuesto, ni unos ni otros notan diferencia alguna en su percepción del paso del tiempo.»
Pingback: Jot Down Cultural Magazine | Miquel Barceló: “En nuestra sociedad mercantilista, si se consigue sacar beneficio de clonar humanos se hará”
Pingback: Entrevista a Miguel Barceló (para Jot Down en 2012) | Sociología crítica