
—Mariano, ¿has visto los resultados del informe PISA?
—Ajá.
—¿Es lo único que se te ocurre decir?
—Hay un tiempo de construir y otro de destruir…
—Eso ya lo dijo José en el Congreso.
—Es verdad. No sé, si la situación es tan desastrosa tendremos que dar un giro de 360 grados a la política educativa, ¿que no?
Evidentemente, es un diálogo ficticio; cualquier parecido con la realidad es eso, un parecido con la realidad. Pero el caso es que, francamente, querida, no me extrañaría que nuestro iluminado presidente del gobierno nos saliera con lo del giro de 360 grados, al más puro estilo Ménem. Claro que este último se ilustraba leyendo la amplia colección de «libros escritos por Sócrates» y se sentía, a veces, bajo la «espada de Penélope»… Nuestro Mariano solo lee el Marca. Es lo bueno que tiene.
Estoy casi segura, bastante segura al menos, de que mucha gente se lleva las manos a la cabeza o se ríe ante la brutalidad de atribuir textos escritos al filósofo ateniense o de imaginarse a la fiel esposa de Odiseo empuñando la de Damocles. La espada, digo. Lo llamativo, y triste, es que el porcentaje de personas que se escandalizan ante el uso de un giro de 360 grados como sinónimo de cambio radical es, significativamente, mucho menor. Pero eso son matemáticas, pueden argumentar para disculparse, y ellos de matemáticas no entienden. Ea, y ya está.
Saber que girar 360 grados es volver a la posición inicial no creo que sean matemáticas, es cultura general. Y de la más básica, oigan. No saber que 360 grados es una vuelta completa es casi como ignorar que antes de b se escribe m. Y sin embargo, a poco que busquen encontrarán artículos periodísticos incidiendo en la mañita de usar el giro completo, es decir, quedarse en el mismo sitio, para indicar una tendencia de cambio radical. Para muestra, un par de botones: «de la realidad de aquellas abuelas a la realidad de las nietas se ha dado un giro de 360 grados» o «el perfil del paciente ha dado un giro de 360 grados: si hace unas décadas la mayoría eran drogodependientes, en la actualidad casi todos los contagios son por transmisión sexual». Sí, son de hace unos días y en ambos casos, se supone, son periodistas.
¿De qué nos extrañamos entonces cuando recibimos los informes sobre nuestro nivel en matemáticas? Es fácil y cómodo culpar a los profesores del fracaso. Total, una hostia más para el gremio, está de moda lincharlos además. El problema no es tan simple, tiene muchísimas caras y todos, absolutamente todos, tenemos nuestra parte de culpa. Pero hoy no voy a hablar de este tema, sino que voy a centrarme en los giros de 360 grados y en un bello problema matemático muy relacionado con ellos. Un problema que me fascina a mí y parece que también a Terence Tao porque, como este último dice, es un problema que a primera vista parece simplemente una curiosidad matemática, sin más, pero que en las últimas décadas se ha usado en ramas muy diversas de las matemáticas con aplicaciones muy interesantes.
Vamos allá.
Supongamos que estamos cansados de nuestra situación actual, que queremos dar un giro a nuestras vidas, radical, a lo loco, de 360 grados (es coña), pero la situación económica del país y las leyes de seguridad ciudadana nos van limitando nuestro espacio vital, ¿hasta cuándo podemos aguantar? ¿Cuánto espacio necesitamos para poder seguir girando 360 grados? ¿Cuál es el área mínima que necesitamos para girarnos?
Como cada uno tenemos nuestra morfología (gordos, delgados, altos, culones…) vamos a tratar una versión más simple del problema: vamos a girar 360 grados una varilla dentro de un recinto, ¿cuál es el área mínima necesaria de dicho recinto para poder asegurar que se puede hacer el giro completo? Estos giros pueden ir acompañados de desplazamientos, nos podemos mover un poco y después seguir girando, como hacemos cuando aparcamos un coche, por ejemplo.
No es difícil pensar que si tengo una varilla de un metro de longitud, esta puede girar en un círculo cuyo diámetro sea también un metro, ¿no? Simplemente, manteniendo fijo el centro de la misma y girando.
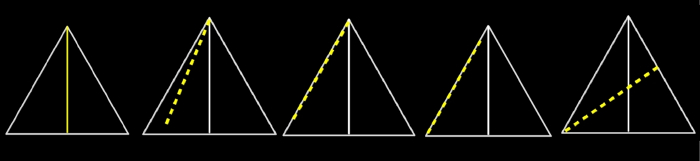
De hecho, se puede hacer con menos área, basta pensar en un triángulo equilátero de altura de un metro, como hemos tratado de explicar en la siguiente ilustración. Nos fijamos en una de las alturas del triángulo (esa será la varilla, en amarillo en el dibujo), la giramos un poco, la llevamos sobre uno de los lados del triángulo, la bajamos hasta el otro vértice del triángulo (el inferior izquierdo en la figura) y la giramos hasta tocar el lado opuesto del triángulo. Siguiendo esta estrategia que, como he dicho, es similar a la que usamos para aparcar el coche en un sitio ajustado, podemos llegar a girar la varilla 360 grados dentro del triángulo.
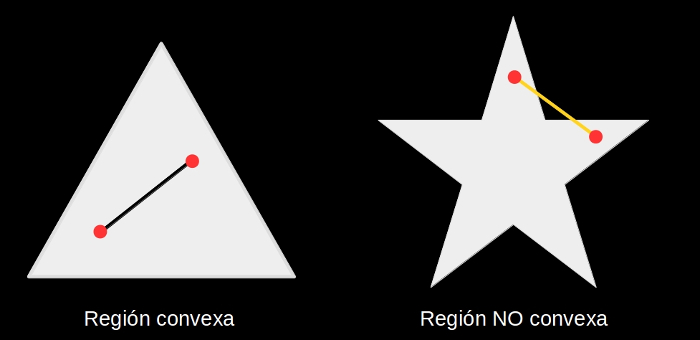
¿Se puede hacer en algún recinto con menor área? Si se exige que el recinto sea convexo, la respuesta es que no: el recinto de menor área en el que se puede girar una varilla de un metro, en estas condiciones (con giros y desplazamientos), es un triángulo equilátero de altura de un metro. ¿Que qué es un recinto convexo? Pues es un recinto en el que cualquier pareja de puntos dentro del mismo se pueden unir con un segmento sin que ese segmento se salga del recinto.
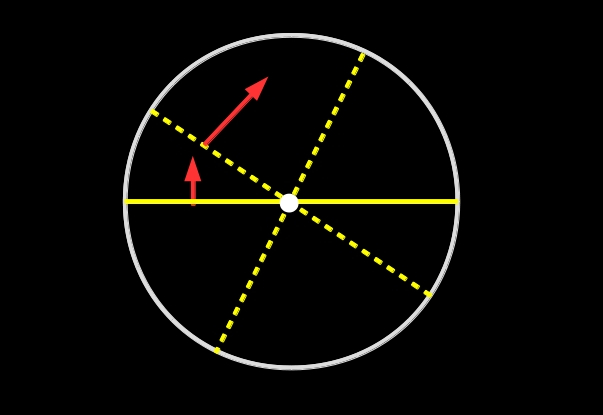
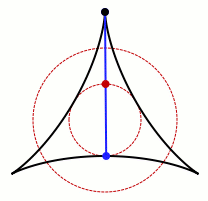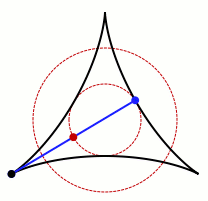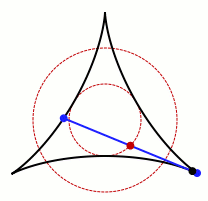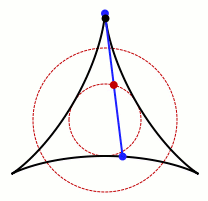
Si no se exige que el recinto sea convexo, el matemático japonés Sōichi Kakeya (que por cierto, fue profesor en Sendai, ciudad a la que los corianos de Coria del Río tenemos gran afecto desde la expedición de Hasekura Tsunenaga), que fue además el que propuso este problema, por ello conocido como el problema de Kakeya, pensaba (o eso se ha dicho por ahí) que el recinto de menor área que permitiría girar una varilla de un metro (permitiendo desplazamientos también) sería un deltoide, como el que aparece en la siguiente animación, en el que la circunferencia dibujada por el punto central de la varilla tiene de diámetro la mitad de la longitud de la misma.
Pero, no, Kakeya se equivocaba si era esto lo que pensaba. Se puede girar la varilla (permitiendo traslaciones, eso sí) en sitios más pequeños. De hecho, se puede encontrar recintos con el área tan pequeña como uno quiera en el que se puede hacer, infinitamente pequeños. Lo sé, es difícil de creer. Pero es verdad. Es lo bueno de las matemáticas, en particular, y de la ciencia, en general: se puede demostrar lo que se afirma: no necesitamos recurrir a la fe ni a la asunción de la memoria del agua.
¿Cómo? A partir de un resultado de Abram Samoilovitch Besicovitch, matemático ruso que trabajó, después de salir sin permiso de su país, entre otros, con Harald Bohr (el matemático futbolista, hermano del ilustre físico) y con uno de mis personajes favoritos en esto de las matemáticas, G.H. Hardy. Otro día hablaremos de este último.
Pues bien, lo que este matemático ruso probó, es que sea cual sea el número positivo que nos den, por muy pequeño que sea, existe un recinto de área menor que dicho número en el que la varilla puede girar. A los conjuntos con esta propiedad se les ha llamado, en un alarde de inventiva, conjuntos de Kakeya. En realidad, la propiedad que tienen los conjuntos descritos por Besicovitch es que en ellos podemos colocar una varilla de un metro, por ejemplo, en cualquier dirección. Pero a partir de estos, de los conjuntos de Besicovitch, se pueden construir conjuntos de Kakeya.
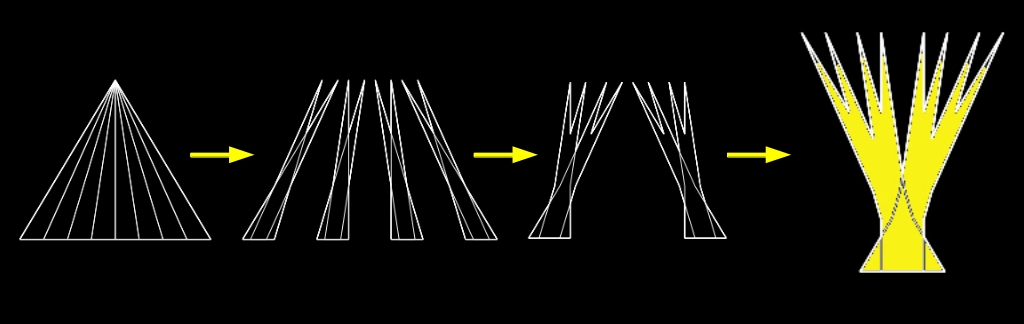
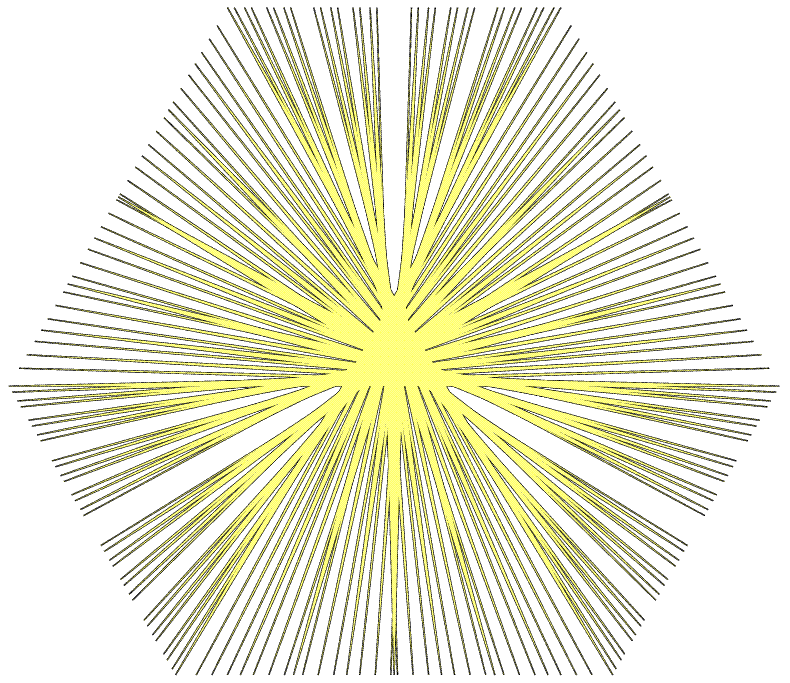
De lo que se trata es de saber construir estos conjuntos con el área tan pequeña como queramos. Uno de los métodos más conocidos para ello es el propuesto por otro matemático, esta vez alemán, Oskar Perron en un trabajo de 1928, en el que simplifica la propuesta del ruso para ello. La construcción de Perron, conocida como el árbol de Perron, consiste en partir de un triángulo equilátero de altura un metro y dividirlo en un número suficiente de triángulos iguales, para luego superponer convenientemente dichos triangulos, de forma que dentro de la figura así obtenida quepa una varilla de un metro de longitud en cualquier dirección. Cuantos más divisiones hagamos del triángulo original, menos área tendrá la figura (el árbol) resultante de las superposiciones.
Luego se rota el árbol y se llega a conjuntos de Besicovitch tan espectaculares como el siguiente:
Básicamente, para girar la varilla en este conjunto lo que hacemos es similar a las maniobras que realizamos con nuestro coche para tratar de aparcarlo en hueco estrecho: giramos un poco, marcha atrás, giramos otro poco, marcha adelante… ya saben.
No me negarán que el resultado es cuanto menos sorprendente, ¿no? Este problema me lo contó Jin Akiyama, de la Tokyo University of Science, uno de los divulgadores más famosos del mundo o, al menos, quien más gente conoce, porque en Japón lo paran por la calle ¡para pedirle autógrafos! Como aquí, vaya… A lo mejor tiene que ver el hecho de que este señor, Akiyama, tiene un programa de divulgación de las matemáticas en la cadena de televisión más importante de Japón (la NHK), en prime time y desde el año 1991… Como decía aquella canción: Japón, mira que nos queda lejos Japón… ay. Pero nosotros somos campeones del mundo de fútbol, coño.









Según la divulgación científica española con más presencia en los medios lo primero que tendríamos que preguntarnos es si la varilla de un metro es feliz.
Por cierto recuerdo con cariño mi primer giro de 360 grados, fue Nieves Herrero, en uno de aquellos programas de Hermida, hablando de no sé qué desgracia.
Lo que más me sorprende es que, según ese enunciado, «sea cual sea el número positivo que nos den, por muy pequeño que sea, existe un recinto de área menor que dicho número en el que la varilla puede girar»… Si lo he entendido bien, eso significaría que el área mínima, en el límite, debería tender a cero. ¿Es así? Perplejo me quedo… 0_0
Sé que es un tema viejo, pero contesto igual.
Entiendo que si en lugar de llamar al número metro, lo llamamos unidad, se hace más fácil de entender que es simplemente una cuestión de escala.
Sí, el límite del área es cero, pero no vale con área cero. Solo vale con un área tan pequeño como queramos.
Efectivamente, Luis, es así :)
Peo, si yo también lo he entendido bien, el acercarnos a cero conllevaría que el numero de movimientos (maniobras) para poder dar el giro de 360º aumentaría, es decir que este en el límite tiende a infinito. O no y no me he enterado de nada? (que tampoco seria raro…)
Y después de esto, creo que habría que hablar de los Fractales, de los que la construcción mostrada parece ser un ejemplo. pero el cerebro de algunos no.
Cuanto ganaríamos si hubiese más divulgadores científicos como tú Clara!!!
Y lo dice uno al que nunca le gustaron demasiado las matemáticas (estudiandolas a conciencia en la carrera) y ahora les está cogiendo el puntillo gracias a tus artículos!
¿Como puedo mover (técnicamente) la varilla, si es exactamente el diámetro o la altura del triángulo?
mucho me temo que ese exactamente solo existe en tu cerebro o en tu nunca suficientemente preciso aparato de medida. Además estas dando un grosor también inconsciente a tu varilla, cuando para cumplir con los supuestos es claramente una linea.
Son los peligros de pensar en algo físico. Si lo que quieres es saber como se puede realizar la operación físicamente te recomiendo cualquier libro de dibujo técnico nivel universitario. Busca el capitulo de juegos y aprietes y te solucionara un poco el tema.
Clara, ¡yo te pararía para pedirte un autógrafo! Eres la caña.
Hola Clara, esclarecedor articulo, pero el armario que estoy moviendo en la habitación no ha leido tu articulo y no quiere girar ¡ ja , ja
Gracias por hacerme pensar en cosas mas didacticas que el euribor.
Saludos
Como uno de tantos analfabetos en matemáticas (sí, soy uno de esos desgraciados «de letras» al que le hubiera gustado tener una mente más despierta para acordarse de las cosas «de ciencias», que me fascinan y se me olvidan del mismo modo), le doy las gracias por el artículo. Me lo he pasado muy bien leyendo, he aprendido algo y me he reído bastante con: «Pero nosotros somos campeones del mundo de fútbol, coño.» ¡Menudo final triunfante, tan castizo -en el buen sentido! Yo también quisiera un programa de matemáticas en la programación televisiva (bueno, y uno de historia que mereciera la pena y no los bodrios que plantan, basados en la idea de que el espectador es imbécil).
Un saludo y muchas gracias por los textos
VEAN POR GOOGLE LAS FALACIAS DE KURT GODEL Y COMPRENDERAN DONDE NO ESTA EL INFINITO CON SOLO DOS LOGICAS MADRE Y OTRAS MUCHAS COSAS.UN SALUDO CLARA
Pingback: Clara Grima explica o Problema de Kakeya | Debuxo na rede
Clara, da grima que todos los ejemplos en los que introduces la política, que no son pocos, dispares siempre contra la derecha. Las reformas educativas que se han aplicado en este país han sido únicamente las del partido socialista. No creo que se pueda acusar a la derecha de sus penosos resultado.