
Hace unos días Josep M. Casacuberta publicaba un artículo en Materia titulado «Por la ciencia, contra la excelencia». En dicho artículo reflexionaba sobre el uso del factor de impacto de las revistas como método de valoración de los científicos. Indicaba el autor que la excelencia y la calidad no son sinónimos, y que con la excusa de primar la excelencia, se está recortando la ciencia española de calidad, y que deberían existir «muchos científicos que trabajen con objetivos más amplios que los de competir para publicar en las revistas de más impacto; científicos que consideren que su trabajo es colaborar para difundir este conocimiento a la sociedad».
Por tanto, ¿cómo se valora a los científicos y qué es el factor de impacto?
El factor de impacto
El factor de impacto intenta medir la repercusión que ha obtenido una revista en la comunidad científica y, teóricamente, refleja la importancia de una publicación a nivel mundial. Este es un instrumento que se utiliza para comparar revistas y evaluar la importancia relativa de una revista concreta dentro de un mismo campo científico.
El problema llega cuando se trata de calcular dicho parámetro, ya que, aunque existe un método de cálculo del factor de impacto, la medida parece no ser lo suficientemente transparente ya que está condicionada a una serie de parámetros, algunos de ellos poco claros. Según rezan las webs de referencia, el factor de impacto de una revista se calcula de la siguiente forma:
Es decir, imposible de calcular de una forma evidente. Para obtener este parámetro, deberíamos hacer un seguimiento de todos y cada uno de los artículos publicados en una revista, estudiando el número de veces que han sido citados en los dos años anteriores, y que a su vez deberíamos dividir por el número total de artículos publicados en esa revista durante esos dos años. Si en cada revista se publican al menos cientos de artículos por año, entonces la tarea empieza a ser ciclópea. Y esto lo tendríamos que hacer para cada revista de la que quisiésemos averiguar el factor de impacto. Materialmente imposible, por lo tanto. Así que existen webs que nos dicen directamente el factor de impacto de cada revista. Eso sí, nos tenemos que fiar.
El índice h
Otra forma de medir la contribución de los científicos es el índice h. Dicho índice, que fue propuesto por Jorge Hirsch de la Universidad de California, mide la calidad de los científicos, que no de la revista en la que publican, determinando la cantidad de citas que han recibido sus artículos científicos. Un científico tiene índice h si ha publicado h trabajos con al menos h citas cada uno. Es decir, un científico con una publicación citada una vez tendría un h=1, pero para tener un h=2 el investigador debería haber publicado al menos dos artículos que al menos hubieran sido citados dos veces cada uno. Es decir, llegados a un cierto valor, aumentar el índice h resulta altamente complicado.
Con este índice no se premia el gran hallazgo científico (digamos el «eureka»), sino que se valora la carrera del investigador de una forma más continua. El impacto real que produce un nuevo descubrimiento se refleja con mayor claridad en el número de veces que se referencia el artículo, antes que en el índice de impacto de la revista donde haya sido publicado.
El número de oro
Sea como fuere, los índices anteriores no son más que meros indicadores de la calidad de una revista o de la carrera profesional de un científico. Pero creo que esta no es la cuestión clave en esta discusión. El punto a evaluar para alcanzar una determinada meta científica o técnica, o para generar suficiente ecosistema investigador en una determinada sociedad o en una región concreta, debería acercarse más a las proporciones relativas del número de oro antes que a los indicadores anteriormente mencionados. Me explico. El número aúreo, también conocido como la divina proporción y representado por la letra griega Φ, es un número crítico, y tal vez mágico, en el diseño de la naturaleza, en la arquitectura desde los tiempos primigenios, y ha sido intencionadamente escondido en cuadros crípticos a lo largo de la historia, como en Las Meninas de Velázquez o en La Gioconda de da Vinci.
Los sacerdotes egipcios utilizaron el número de oro para el diseño de sus pirámides hace más de tres mil años. Curiosamente, la apotema lateral de una pirámide (la altura de una de sus caras) dividido por la mitad de la cara de la base es Φ. Además, el cociente entre el área total y el área lateral de una pirámide es 1,618. No acaba aquí la cosa. El cociente entre el área lateral y el área de la base es el número aúreo.
Pirámides y científicos
En resumen, y haciendo una asunción de lo más banal, pero a la vez de lo más cierta: cuanto más grande es la base de una pirámide cuadrangular normalmente más altura alcanza. ¿Y adónde nos lleva este hecho en el tema que nos ocupa? Pues muy sencillo, las grandes cotas se alcanzan a partir de un amplio asentamiento que soporte dicha altura. Puro cálculo de estructuras. Y en ciencia las cosas son exactamente así. Para tener grandes descubrimientos (es decir, publicaciones en revistas con altos factores de impacto) o grandes científicos (investigadores con altos índices h) necesitamos una gran base que se asiente sobre muchos obreros de la ciencia, con la mayor capacidad productiva posible y, por supuesto, con la mayor de las calidades en sus desarrollos. Matemos pues desde ahora mismo el refrán de la cabeza de ratón y de la cola de león que tanto daño ha hecho a la ciencia española en la última década. No pueden existir leones si no hay ratones a los que se puedan comer. El ecosistema científico debe sustentarse en el equilibrio natural de muchos pequeños animales y de algún león, tal vez blanco.
Epílogo
El área de la base de la pirámide no puede considerarse de igual forma que su vértice: su altura tiende a cero, mientras que la carga que soporta tiende a infinito. La base de la ciencia debe sustentarse en grupos de investigación más competitivos y con cierta orientación a servicios, en una fuerte divulgación de la ciencia y de la tecnología orientada al gran público (tanto de investigadores especializados como de profesionales de la comunicación específicamente formados), en estrechas relaciones con otros actores del sistema de I+D (por ejemplo asistenciales), en una cultura de valorización de tecnologías y de su evolución a patentes y licencias, y en la creación de spin-offs y empresas de valor. Sólo de esta forma tendremos grandes científicos y brillantes descubrimientos y, tal vez, algún día otro premio Nobel.




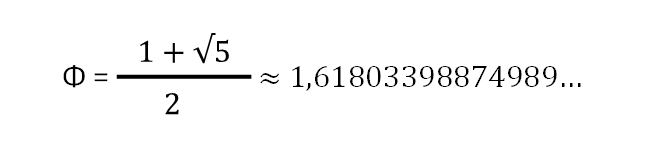






Señores, el artículo hace de buen leer y la proporción áurea es interesante sin duda pero me temo que lo que aquí se dice sobre su uso por parte de los egipcios y por parte de Da Vinci en la Gioconda no es más que una patraña que se va repitiendo por inercia. Hay bastantes académicos que llevan tiempo diciéndolo.
http://www.umcs.maine.edu/~markov/GoldenRatio.pdf
http://www.maa.org/external_archive/devlin/devlin_05_07.html
Pingback: De pirámides, científicos y la divina proporción
Pingback: Bitacoras.com
Pingback: Artículo en Jot Down (noviembre 2013) | El león blanco
Tras la publicación del artículo han surgido dudas sobre las afirmaciones realizadas en el texto en la relación del número Φ con las diferentes ratios de las medidas de las pirámides. Me gustaría intentar resolver dichas dudas. La mejor forma que se me ocurre es haciendo los cálculos sobre las dimensiones de la Gran Pirámide de Keops. Los datos que necesitamos para los cálculos son los siguientes:
Apotema = 186,43 m
Arista = 219,14 m
Lado de la base = 230,35 m
Con estos datos podemos calcular las siguientes áreas:
Área de la base (de un cuadrado, puesto que es cuadrángular) = lado x lado = 230,35 x 230,35 = 53.061,12 m2
Área de una cara lateral (de un triángulo) = (base x altura)/2 = (lado x apotema)/2 = (230,35 x 186,43)/2 = 21.472,08 m2
Área lateral (de las 4 caras) = 4 x 21.472,08 = 85.888,30 m2
Área total = Área lateral (de las 4 caras) + Área de la base = 53.061,12 + 85.888,30 = 138.949,42 m2
Ahora veamos si las afirmaciones del artículo son correctas:
«la apotema lateral de una pirámide (la altura de una de sus caras) dividido por la mitad de la cara de la base es Φ.»
Apotema/mitad del lado de la base = 186,43/115,18 = 1,618
«Además, el cociente entre el área total y el área lateral de una pirámide es 1,618.»
Área total/área lateral (de las 4 caras) = 138.949,42/85.888,30 = 1,618
«El cociente entre el área lateral y el área de la base es el número aúreo»
Área lateral (de las 4 caras)/área de la base = 85.888,30/53.061,12 = 1,618
Por lo que las afirmaciones son correctas.
Soy @felpalgon. Llevas toda la razón, yo estaba equivocado. Pero también es verdad que «apotema/mitad del lado de la base» siempre es igual a «área lateral/área de la base» (es la redundancia que yo me refería). Por que, al final, son dos ecuaciones con una incógnita. Si se cumplen, es por que hay dos relaciones que son iguales. La clave es «área total/área lateral», igualando ésta a una de las otras ya obtenemos «n°áureo = 2*apotema/lado de la base» como única solución del problema. Ciertamente mi error estuvo en considerar área lateral como el área de una sola cara triangular y no de las 4.
PD: Yo soy más de hacer cuentas con letras y no con números.
Un saludo
Señor Burgos, lamento ser agrio en mis comentarios pero estaría bien leer el artículo que citaba antes de responder a mi comentario.
La proporción áurea tiene una importancia histórica indudable pero no hay constancia histórica fiable sobre su uso hasta muchos siglos más tarde (http://en.wikipedia.org/wiki/Golden_ratio#History).
No discutimos si esos números en la pirámide dan lo que dan, discutimos si la razón por la que dan lo que dan es porque los egipcios usaron la proporción áurea para diseñar las pirámides o dan lo que dan por cualquier otra razón. Examinando las dimensiones de las pirámides se pueden encontrar otras coincidencias igualmente opinables. Aquí tiene un puñado: http://books.google.co.uk/books?id=066T3YLuhA0C