Este artículo ha sido finalista del Concurso de divulgación Ciencia Jot Down con la temática «orden y caos» en la modalidad de ensayo
Mi querido amigo, tengo el honor de enviarle adjunto un cheque por valor de 3.585 coronas, del que le ruego acuse recibo.
…
Su devoto amigo, Poincaré
Así escribía Henri Poincaré al matemático sueco Gösta Mittag-Leffler el 1 de junio de 1890. El cheque correspondía a los gastos de reimpresión del artículo titulado “Sobre el problema de los tres cuerpos y las ecuaciones de la dinámica” en la revista Acta Mathematica y tenía ni más ni menos que 227 páginas.
Pero vayamos al principio. Mittag-Leffler había persuadido al rey de Suecia Óscar II para que convocara un premio entre los matemáticos de toda Europa con motivo de su 60 cumpleaños, en enero de 1889. El rey era un amante de las matemáticas y accedió a la petición de Mittag-Leffler prometiendo 2.500 coronas suecas al ganador, junto con una medalla de oro con la efigie del rey. El trabajo ganador sería publicado en un número especial de la revista Acta Mathematica. Los trabajos tenían que versar sobre uno de cuatro temas propuestos, entre los cuales se encontraba la estabilidad del sistema solar. Y este fue el tema escogido por Poincaré para presentarse al premio. Y ganó.
Aunque Newton había demostrado que un planeta sometido a la atracción gravitatoria del Sol describe una trayectoria elíptica cerrada de forma exacta, él mismo comprendió que la presencia de los otros planetas influiría sobre la órbita, pudiendo desestabilizarla. Bastantes años después el matemático francés Pierre Simon de Laplace demostró que la influencia de otros planetas introduciría oscilaciones periódicas en las órbitas elípticas, pero no las romperían. Es decir, el sistema solar era estable y los planetas se moverían en sus órbitas elípticas, ligeramente perturbadas, por los siglos de los siglos.
Pero esta conclusión de Laplace fue puesta en duda en las décadas siguiente por otros grandes matemáticos, y para finales del siglo XIX la cuestión no se consideraba resuelta. Poincaré abordó el problema con motivo del premio del rey de Suecia y llegó a la conclusión… de que no había conclusión. De entrada, Poincaré no analiza el sistema solar entero, sino que se restringe al problema de los tres cuerpos en mutua interacción gravitatoria. Y aún más, se limita al caso en el que uno de los cuerpos tiene masa despreciable y los otros dos describen trayectorias circulares, siendo uno de ellos mucho más masivo que el otro. Como demuestra, este problema tan simplificado es ya demasiado complicado. En palabras del mismo Poincaré: «Muchas otras circunstancias nos hacen prever que la solución completa, si alguna vez se encuentra, requerirá instrumentos analíticos absolutamente diferentes de los que tenemos e infinitamente más complicados. Cuanto más se piensa sobre las proposiciones que demuestro más adelante, mejor entenderemos que este problema presenta dificultades sin precedentes…». Poincaré acierta de pleno. Por un lado, durante todo el siglo XX se desarrolló lo que conocemos como teoría de sistemas dinámicos, de la que el trabajo de Poincaré es precursor. Y, por otro lado, la aparición de los ordenadores y los métodos numéricos de computación ha sido imprescindible para comprender muchas de las propiedades de las soluciones de sistemas de ecuaciones similares a los de los tres cuerpos. Así, hoy día se hacen simulaciones por ordenador del movimiento del sistema solar en su totalidad. Y por ello sabemos que se trata de un sistema caótico. Pero este caos se manifestará en escalas de tiempo muy largas, de miles de millones de años, por lo que no hay que preocuparse por ello, de momento.
El problema de los tres cuerpos es un ejemplo de caos determinista y Poincaré fue el primero en intuirlo. Por caos entendemos que el sistema se comporta de forma errática y casi aleatoria. El término determinista hace referencia a que, a pesar de ese comportamiento errático, está sometido a leyes bien definidas y determinadas.
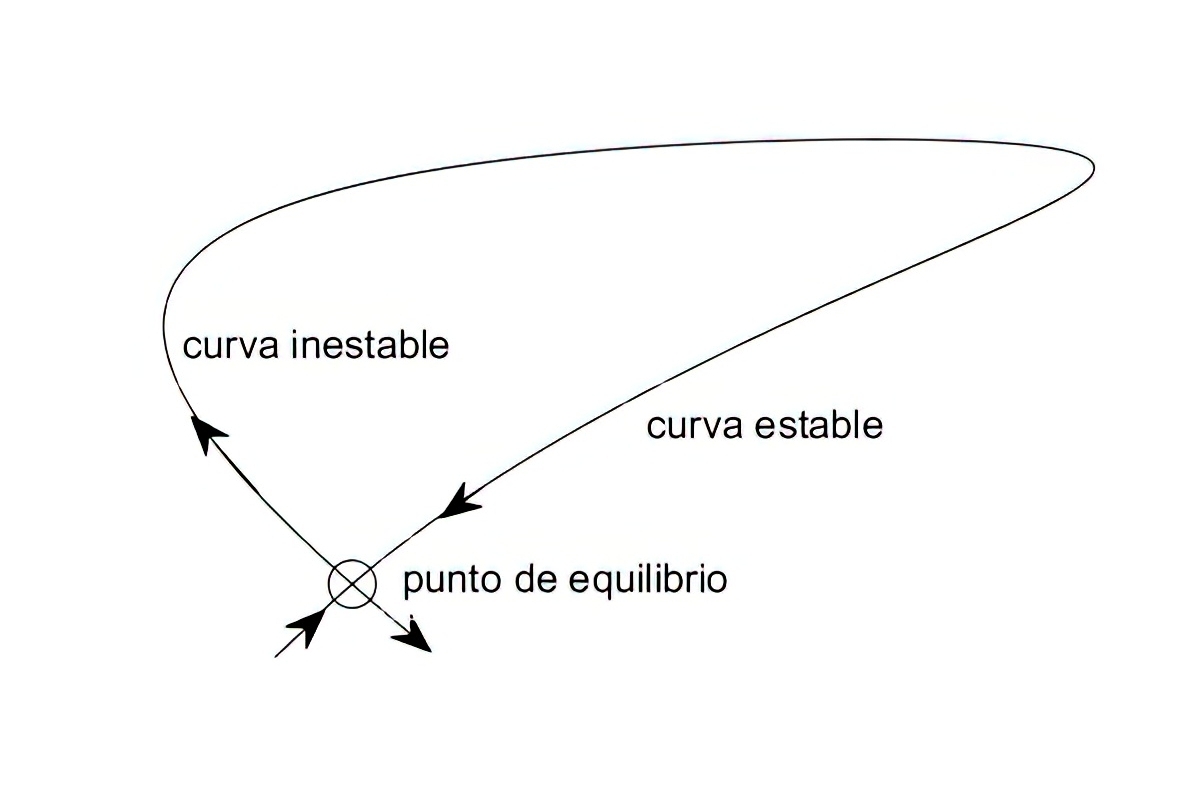
En una de las secciones de su trabajo para el premio Poincaré analizaba el comportamiento de trayectorias como la de la figura 1, y que él mismo llamó homoclina. El punto marcado con un círculo es un punto de equilibrio del tipo punto de silla. Un cuerpo que estuviera cerca de este equilibrio tendería a acercarse a él según una dirección, pero tendería a alejarse por otra. En la homoclina la trayectoria saliente se convierte en entrante.
En un primer análisis Poincaré creyó que las perturbaciones no destruirían la homoclina. Esta se deformaría ligeramente, pero la curva saliente seguiría coincidiendo con la entrante. Así figuraba en la memoria original enviada al jurado del premio del rey de Suecia. Pero, una vez otorgado el premio y durante la revisión de la memoria en el proceso de edición, el matemático sueco encargado de ello por Mittag-Leffler, Lars Edvard Phragmén, preguntó a Poincaré por esta cuestión, pidiéndole que ampliara el argumento. Y Poincaré se dio cuenta de que se había equivocado. En una carta del 1 de diciembre de 1889 escribió a Mittag-Leffler:
Mi querido amigo: escribí al Sr. Phragmén para hablarle de un error que yo había cometido y sin duda él os ha comunicado mi carta. Pero las consecuencias de este error son mucho más graves de lo que había creído en un principio.
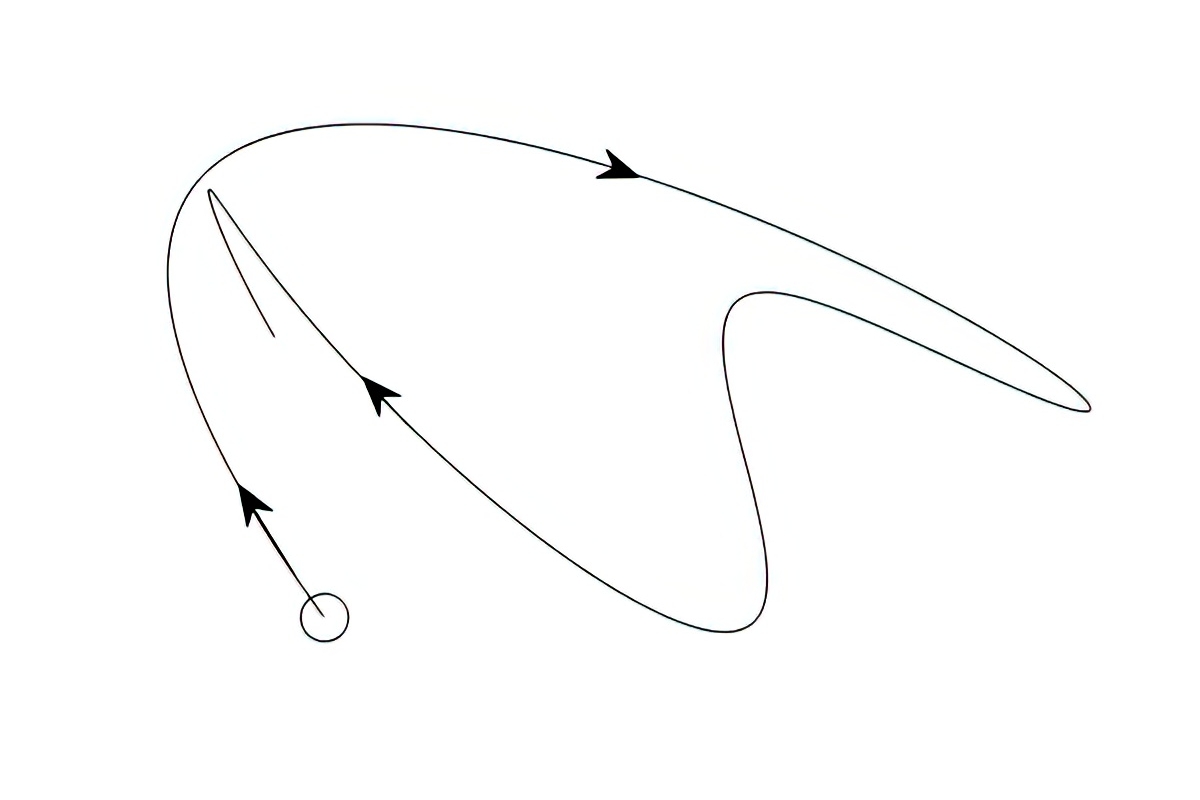
Poincaré comprendió que la homoclina se rompía. La curva saliente, rama inestable del punto de silla, no coincide con la curva entrante, rama estable. La rama inestable tiende a volver al punto de silla, pero se acerca y se aleja en zig-zag, dando excursiones cada vez más alejadas, como se muestra en la figura 2. Poincaré lo describe así años más tarde en su libro Los nuevos métodos de la mecánica celeste:
…esta figura formada por dos curvas y sus intersecciones en número infinito, cada una de las cuales corresponde a una solución doblemente asintótica, estas intersecciones forman una especie de enrejado, de tela o malla infinitamente tupida; cada una de estas curvas no se cortan nunca consigo mismas, pero deben replegarse sobre sí mismas de manera muy compleja, para volver a cortar una infinidad de veces las fibras de la malla. Nos sorprenderá la complejidad de esta figura, que ni siquiera trato de dibujar.
Yo he dibujado parte de estas dos curvas con ayuda del ordenador en la figura 3. Se adivina la forma intrincada que se produce cuando calculamos más y más trozos de estas curvas. Esta estructura se conoce como enredo homoclino. Un objeto que siga una trayectoria en esta zona del espacio se moverá de forma errática.

Mittag-Leffler no ocultó su disgusto con la situación creada. La memoria original ya había sido imprimida y estaba lista para su distribución, por lo que el dinero presupuestado para ello ya había sido gastado. Por ello pidió a Poincaré que se hiciera cargo de los gastos de edición e impresión de la memoria corregida. Y esa es la razón por la que Poincaré le enviaba 3.585 coronas en la carta que he reproducido al principio. Así que no se puede decir que Poincaré hiciera un buen negocio: recibió 2.500 coronas, del premio, pero tuvo que poner 3.585, por la reimpresión. De todas formas, la obtención del premio tuvo gran repercusión en toda Europa, y en Francia el gobierno otorgó a Poincaré la Legión de Honor. Y, lo que quizás sea más importante, la detección del error llevó a Poincaré a un descubrimiento mayúsculo, que dotaba a su trabajo de una repercusión aún mayor. En fin, ¿cuánto vale pasar a la historia?
El movimiento planetario está determinado por las leyes de movimiento de Newton y su ley de la gravedad. Todo ello se traduce en un conjunto de ecuaciones que los matemáticos llaman diferenciales. Este tipo de ecuaciones se aplica no solo al movimiento planetario, sino a una gran variedad de sistemas. Poincaré comprendió que, en casos como el problema de los tres cuerpos en que no es posible una solución explícita y cerrada, era importante tener una comprensión al menos cualitativa de cómo se iba a comportar el sistema en su globalidad. Esta idea le llevó a desarrollar métodos cualitativos y, más tarde, le llevaría a la topología, toda una rama de las matemáticas.
Los conceptos desarrollados por Poincaré se aplican a cualquier sistema cuya evolución pueda expresarse en términos deterministas. En realidad, las figuras 1, 2 y 3 no las he obtenido resolviendo las ecuaciones del problema de los tres cuerpos. Corresponden a un problema más sencillo: el de una pelota que bota sobre una superficie oscilante. Cuando la pelota bota sale disparada hacia arriba y la ley de la caída de los cuerpos nos dice cuánto va a tardar en volver a golpear la superficie. Dependiendo de la velocidad de la superficie en el momento del impacto la pelota rebota con una u otra velocidad. Utilizando toda esta información obtenemos dos ecuaciones algebraicas que nos dan la velocidad de la pelota y el tiempo de impacto en función de la velocidad y el tiempo del impacto anterior. Es lo que los matemáticos llaman una aplicación. Dos parámetros controlan el problema: el coeficiente de restitución, que llamaremos a, y la amplitud de las oscilaciones de la superficie, que denotaremos por g. El coeficiente de restitución es el cociente entre la velocidad relativa de la bola respecto de la superficie después del choque y antes del choque. Si a vale 1 la bola no pierde nada de su energía al chocar y sale con la misma velocidad, respecto de la superficie, que traía antes del choque. Si el coeficiente vale 0 la bola se frena totalmente y se queda pegada a la superficie. Para valores intermedios la bola pierde parte de su energía en el choque.
Las figuras 1, 2 y 3 corresponden al caso en que a vale 1. A todos los efectos esta situación es la misma estudiada por Poincaré para el problema de los tres cuerpos y sus intuiciones sobre el enredo homoclino se aplican de lleno a la bola que bota. El parámetro g controla la perturbación. En la figura 1 g vale 0,2. En las figuras 2 y 3 vale 1,8.
Pero si analizamos el problema para a distinto de 1, el sistema presenta un comportamiento aún más interesante. Y Poincaré también nos ayuda a estudiarlo. Otro de los resultados destacados que el matemático francés describe en su extensa memoria para el premio del rey de Suecia es el teorema de recurrencia. En lo esencial este teorema establece que, para un sistema acotado, esto es, que no se extienda hasta el infinito, las trayectorias vuelven sobre sí mismas tarde o temprano. Este teorema ha inspirado lo que se denominan diagramas de recurrencia.
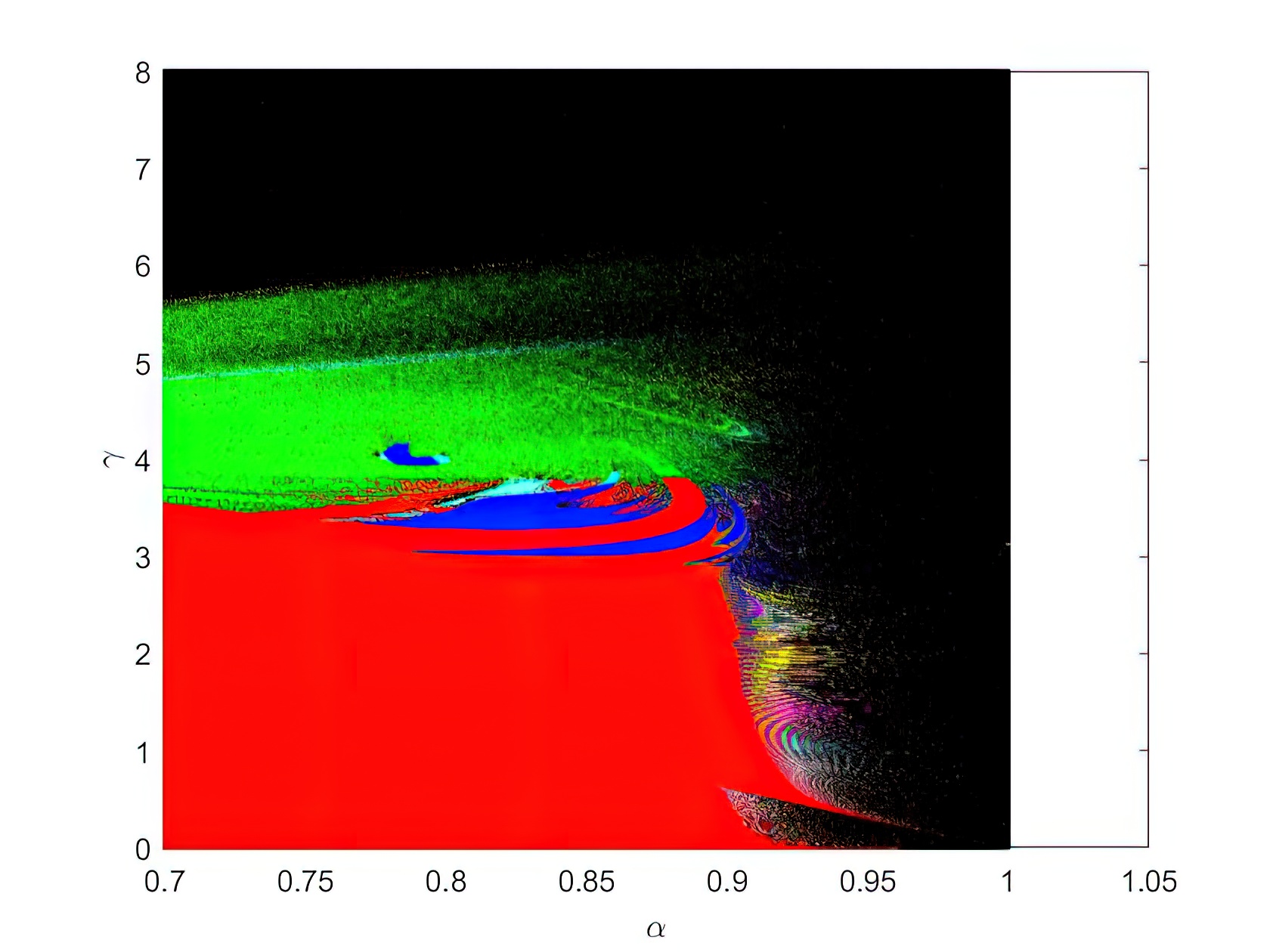
En la figura 4 he representado el diagrama de recurrencia de la bola que bota. En el eje horizontal está el coeficiente de restitución y en el eje vertical la amplitud de las oscilaciones. En cada punto está codificado en colores lo que algunos llaman el tiempo de Poincaré (en nuestro caso es un número natural), porque este tiempo de recurrencia fue definido por él en su artículo.
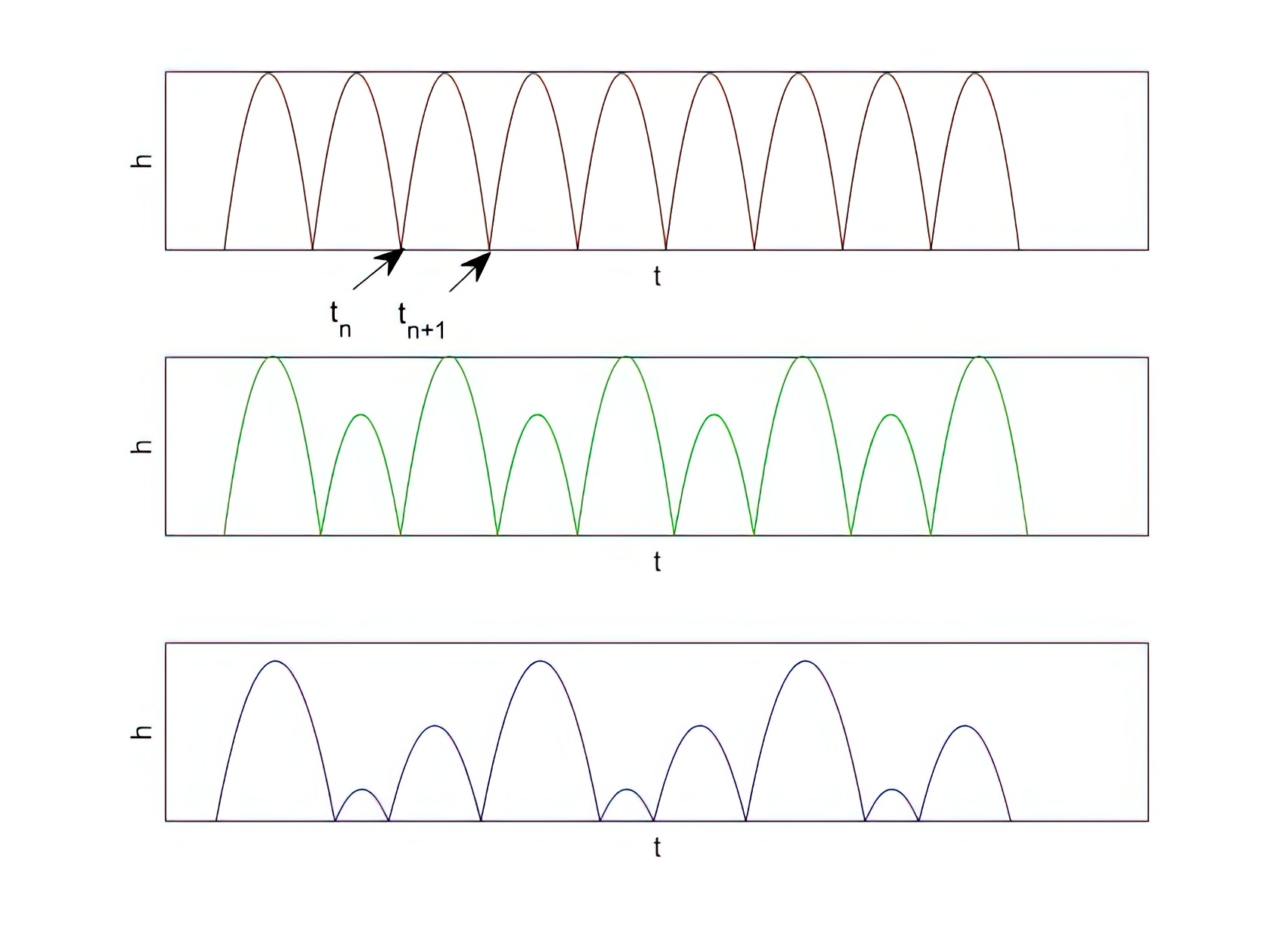
La idea es la siguiente: para un valor dado de a y g, iteramos muchas veces las ecuaciones, obteniendo la velocidad y el instante de sucesivos impactos. Nos fijamos en la velocidad de un impacto dado y la comparamos con la velocidad del impacto siguiente. Si son iguales le asignamos un 1. Si son diferentes, comparamos con el impacto siguiente y si son iguales le asignamos un 2. Si son diferentes, volvemos a comparar con el tercero siguiente, y así sucesivamente. Lo que esto significa en la práctica es que si el número de Poincaré es un 1 los sucesivos botes se producen a intervalos iguales y siempre con la misma velocidad. La bola haría «tic, tic, tic…». Si el número es 2 habrá dos saltos distintos y luego se repetirá el primero: «tic, toc, tic, toc…». Si el número es 3 tendríamos «tic, toc, tac, tic, toc, tac…». Etcétera. En la figura 5 he representado la altura de la bola en función del tiempo para los casos 1, 2 y 3.
He llegado a comparar hasta 8 saltos sucesivos y he asignado el color negro a los puntos con este número de Poincaré o superiores. En la mayoría de los casos en la zona negra el número es mucho mayor que 8, el comportamiento es caótico y la pelota bota irregularmente. Mis cálculos están limitados fundamentalmente por la capacidad de mi PC: los diagramas tienen un millón de puntos.
Una de las características de los sistemas caóticos deterministas, como el de la bola que bota, es que dan lugar a estructuras fractales. La figura 6 muestra una ampliación de una zona de la figura 4. En la figura 4, a varía entre 0,7 y 1 mientras que g lo hace entre 0 y 8. En la figura 6 los límites son 0,87 y 0,9, y 3,5 y 3,9, respectivamente. Y la figura 7 es una segunda ampliación. Las tres figuras tienen el mismo número de puntos. Se observa que, a medida que ampliamos, se van revelando más detalles y las sucesivas ampliaciones muestran estructuras similares. Esta propiedad, en la que sucesivas ampliaciones muestran estructuras similares, se conoce como autosimilaridad.
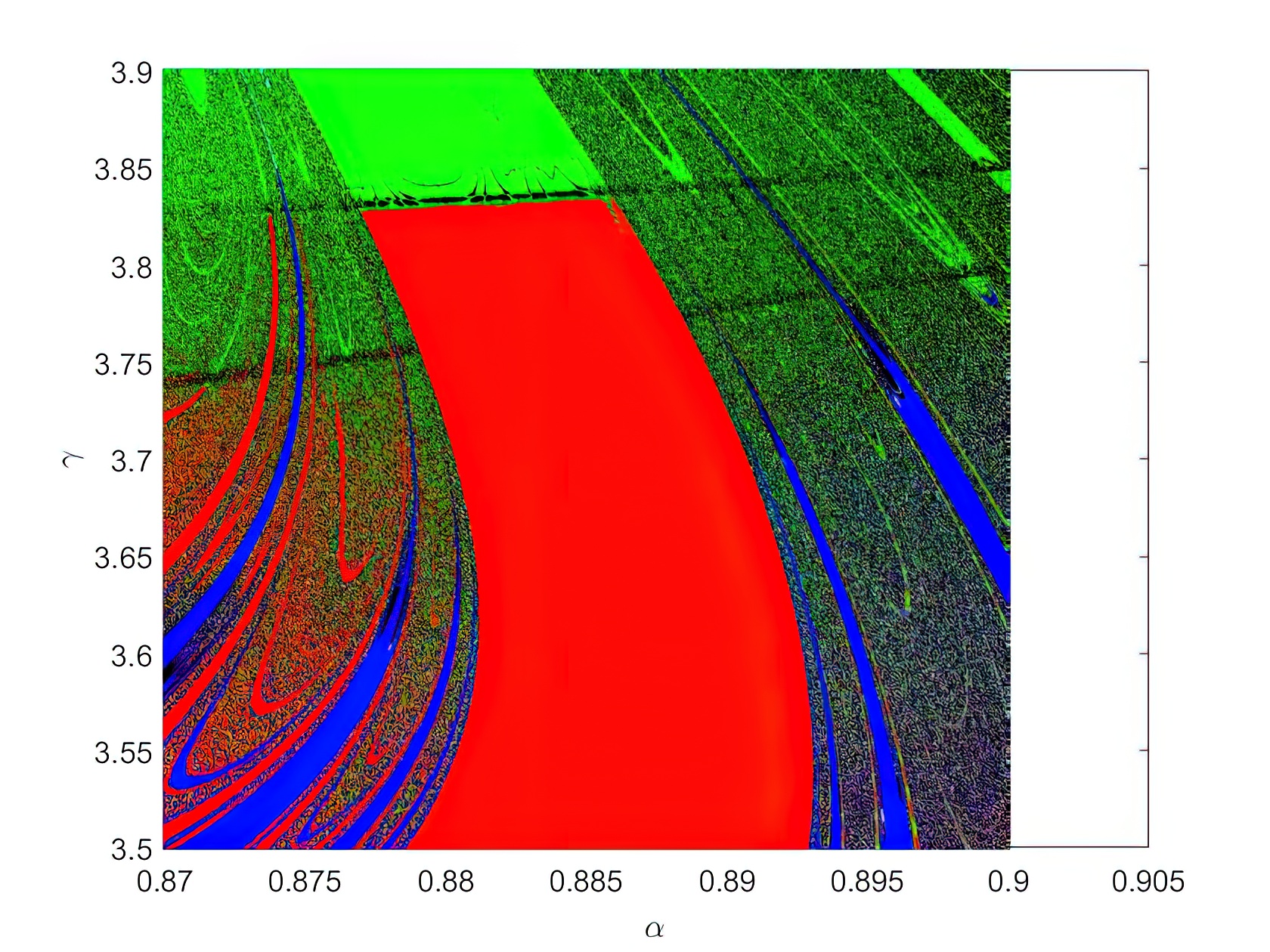
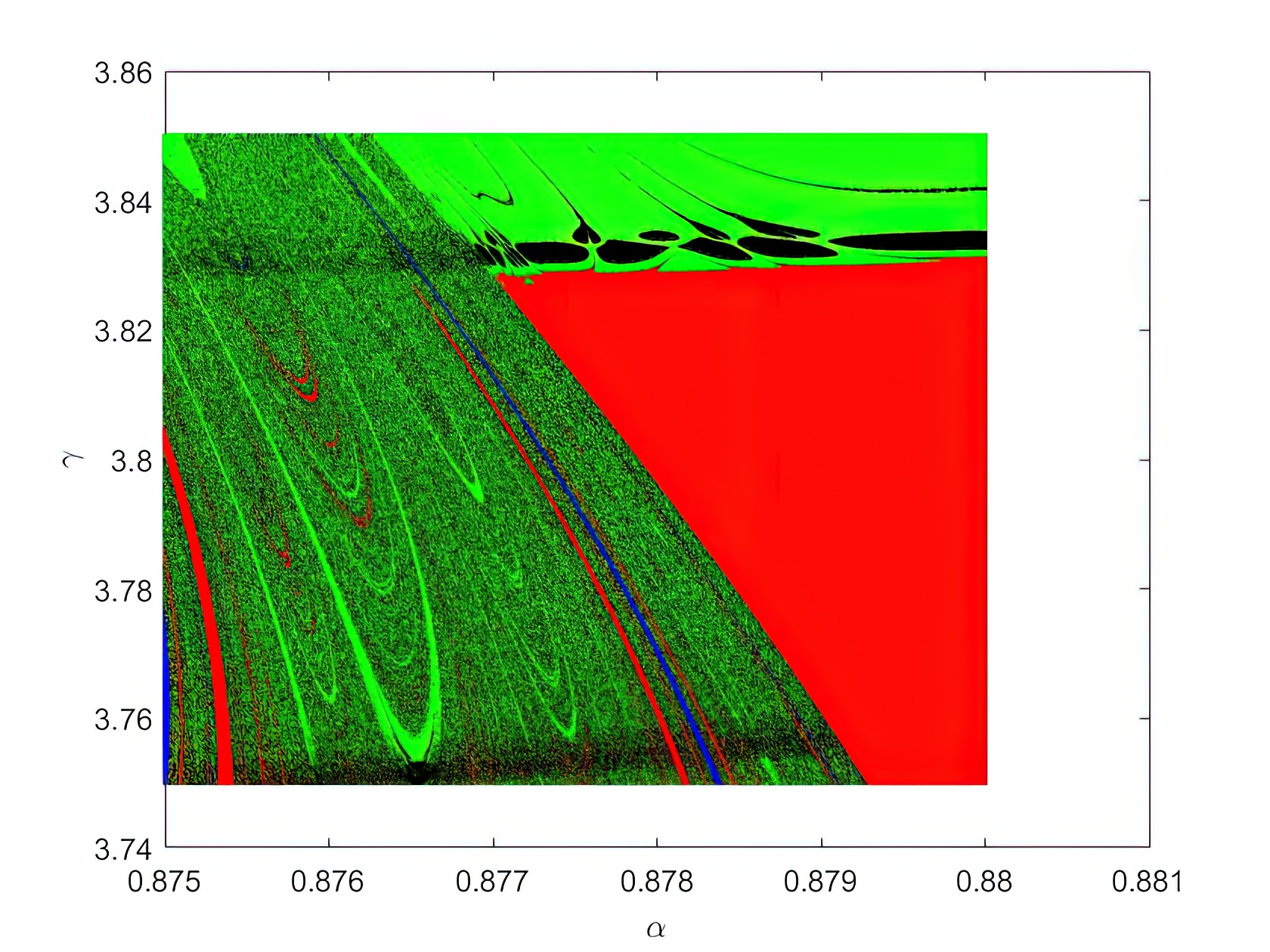
En la figura 4 las zonas más interesantes, donde se manifiestan la fractalidad y la autosimilaridad, son las fronteras entre la región roja y la negra, donde vemos varios colores. Ahí el comportamiento es muy sensible al valor concreto de los parámetros.
La bola que bota sobre una superficie oscilante es un sistema muy sencillo. Tiene dos variables: el tiempo de bote y la velocidad tras el impacto. Y dos parámetros: la amplitud de las oscilaciones y el coeficiente de restitución. Y sin embargo presenta un comportamiento dinámico muy complejo. Es algo que ya vislumbró Poincaré y que físicos y matemáticos desvelaron a lo largo del siglo XX.
Este sistema también ilustra un concepto importante. Tanto la regularidad como la aleatoriedad absolutas son anodinas. En un mundo perfectamente periódico no habría cambios ni evolución. Y en un mundo completamente aleatorio todo intento de aprendizaje o adaptación sería inútil, porque las circunstancias cambiarían caprichosamente. Las cosas interesantes pasan en esa zona intermedia donde el comportamiento no es completamente periódico ni completamente aleatorio. Esa es la zona de la vida, y también la del amor o la desesperación.