
En la entrega anterior usamos el modelo SIR (Susceptibles-Infectados-Recuperados) para hacernos una idea de cómo evoluciona en el tiempo una epidemia como la que estamos sufriendo en la actualidad. Avisábamos también al avispado lector de que un modelo es siempre una simplificación de la realidad y en particular la versión más sencilla del modelo SIR que presentábamos se podría considerar una vaca esférica y sin rozamiento. Es muy fácil de visualizar, dada su sencillez, pero esa misma sencillez tiene un coste en realismo (las vacas distan bastante de ser esferas).
Pues bien, el procedimiento habitual en el negocio de la ciencia es ir refinando los modelos, de tal manera que vayamos ganando en realismo. Hoy proponemos añadir rozamiento a nuestra vaca, examinado el modelo SEIR.
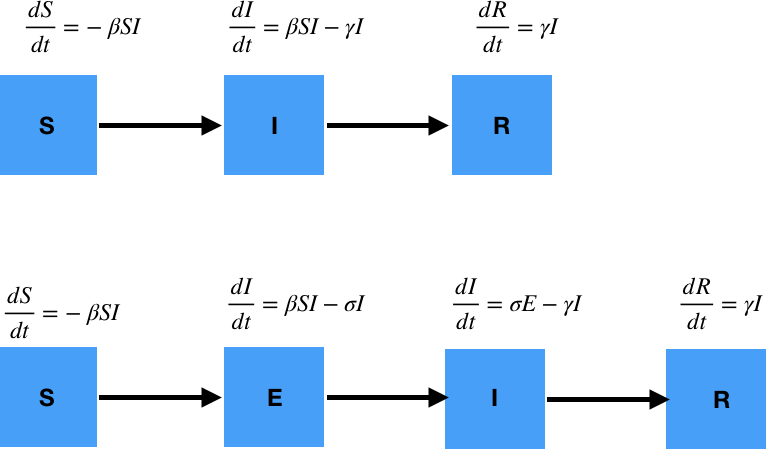
SEIR introduce una categoría más entre Susceptibles e Infectados, que es la de Expuestos. En una enfermedad vírica como la COVID-19, el proceso de transmisión suele iniciarse mediante la inoculación de un pequeño número de patógenos —la microgota que tras un estornudo se transmite al vecino vía boca-mano-mano-boca—. Sigue un periodo en el que el virus se reproduce rápidamente, bajo el radar del sistema inmune. Durante ese periodo la concentración del bicho es demasiado baja para que la persona que lo ha contraído lo transmita a otras por la vías más frecuentes y por tanto, todavía no infecta a otros (por tanto no nos casa en la categoría I) pero tampoco es ya «susceptible» (puesto que ha contraído el patógeno y en consecuencia no nos cabe en la S). Esto nos lleva a introducir una nueva categoría, que refleje la fracción de la población que llamamos «Expuestos». Asociado con esta categoría tenemos un tiempo de incubación de la enfermedad, Ti, y su recíproco, la tasa de infección, s = 1/Ti.
En el modelo SIR teníamos tres ecuaciones que describían la transición entre las categorías S, I y R. En el modelo SEIR, tenemos una ecuación más (figura 1). En este caso, la población de S (susceptibles) disminuye a favor de la población E (expuestos) en lugar de hacerlo directamente a favor de I (infectados). De E a I se pasa mediante una tasa controlada por la inversa del tiempo de incubación (a medida que los expuestos alcanzan dicho tiempo se transforman en infecciosos y saltan de categoría) y de I a R se pasa mediante una tasa controlada por el tiempo de recuperación. SEIR se define por tanto en términos de dos parámetros que ya conocíamos, a saber, la tasa de recuperación (g = 1/T, donde T es el tiempo requerido para recuperarse, o lo que es lo mismo el tiempo que se permanece infeccioso) y el producto de la tasa de contacto y la probabilidad de transmisión (b) —recordemos que el número de reproducción básica se obtiene a partir de estos dos, R0 = b/g—. A estas cantidades añadimos una tercera, la tasa de infección, s (s = 1/Ti, donde Ti es el tiempo de incubación de la enfermedad). En la entrega anterior, tomamos R0=3 y T = 7 días como cantidades que describen (aproximadamente) la pandemia que nos ocupa. Añadimos ahora el tiempo de incubación, Ti = 5 días (s = 1/5) [1].
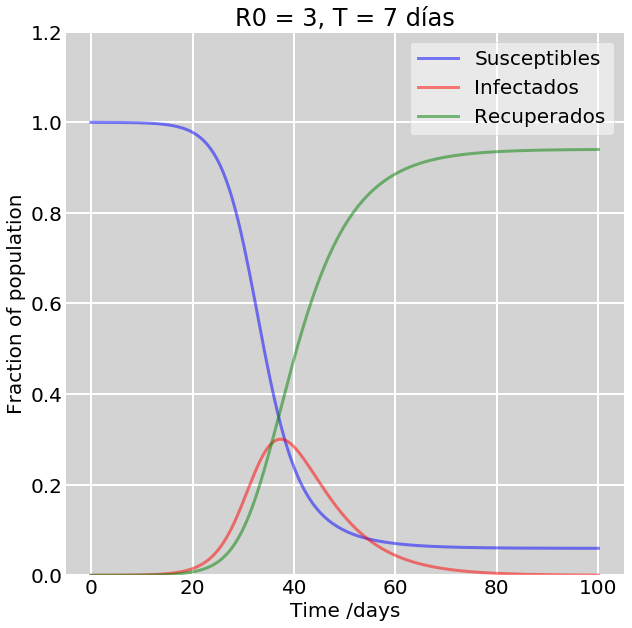
El sistema SEIR puede resolverse con las mismas técnicas numéricas que SIR. La figura 2 muestra una comparación entre los resultados para SIR y para SEIR. Observe el lector que añadir el tiempo de incubación tiene como consecuencia que la curva I (curva roja en ambos modelos) se «aplane» considerablemente. La intensidad del pico ha disminuido casi por un factor 2 (buenas noticias) y llega con un factor dos de retraso (a los 75 días en lugar de a los 35).
Podemos ahora usar nuestra vaca esférica (pero con rozamiento) para intentar entender la situación. Vamos a empezar por examinar dos escenarios. Uno, al que denominaremos temprano (T), en el que se hubieran tomado medidas muy pronto, digamos que el 1 de marzo, cuando el número de casos en España (y en Italia, que llevaba delantera) avisaba claramente de la que se nos venía encima. Y otro, R («retardado» y también «real») que refleja lo que ha ocurrido (medidas tomadas el 15 de marzo).
En el escenario T vamos a suponer que las medidas se toman escalonadamente: La primera semana se prohíben concentraciones de más de mil personas, se suspenden eventos deportivos masivos (partidos de fútbol, etc.) y se recomienda a la población quedarse en casa siempre que se pueda. Vamos a imaginar que esas medidas tienen el efecto de mitigar R0 al 80 % de su valor máximo. La segunda semana se cierran bares y discotecas, así como colegios y universidades. Se recomienda teletrabajar siempre que sea posible y se insiste en la recomendación de quedarse en casa. Supongamos que estas medidas consiguen mitigar R0 al 60 % de su valor máximo durante ese periodo. El 15 de marzo, al igual que ocurre en el escenario R, se adoptan las medidas que todos conocemos. Digamos que R0 se mitiga al 40% de su valor máximo.
En el escenario R, no se hace nada (más bien al contrario) hasta el 15 de Marzo y ahí se aplican de golpe medidas que reducen R0 al 40% de su valor inicial.
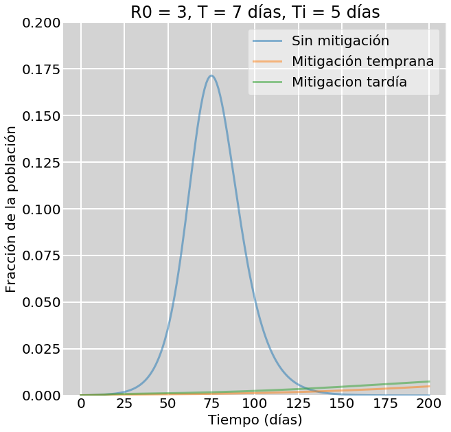
La figura 3 muestra el resultado y no son tan malas noticias. El panel superior compara los escenarios T y R con el escenario en el que no se toman medidas. Observe el lector que las curvas correspondientes a los escenarios mitigados casi no se ven. Primera lección: hacer algo es mucho mejor que no hacer nada. El panel inferior muestra un zoom de las curvas mitigadas (extendidas en el tiempo). La diferencia entre el escenario T y el R no es tan dramática y ambos muchísimo mejores que el escenario sin mitigación. Actuar tarde, en este caso es mejor, muchísimo mejor, que no actuar nunca. Observe también el lector que «el pico» llega muy retrasado, en el rango de los 250-300 días.
¿Pero serán suficientes las medidas que se han tomado? ¿Pueden relajarse? ¿Hay que endurecerlas? Para hacernos una idea podemos usar una vez más nuestra vaca esférica SEIR.
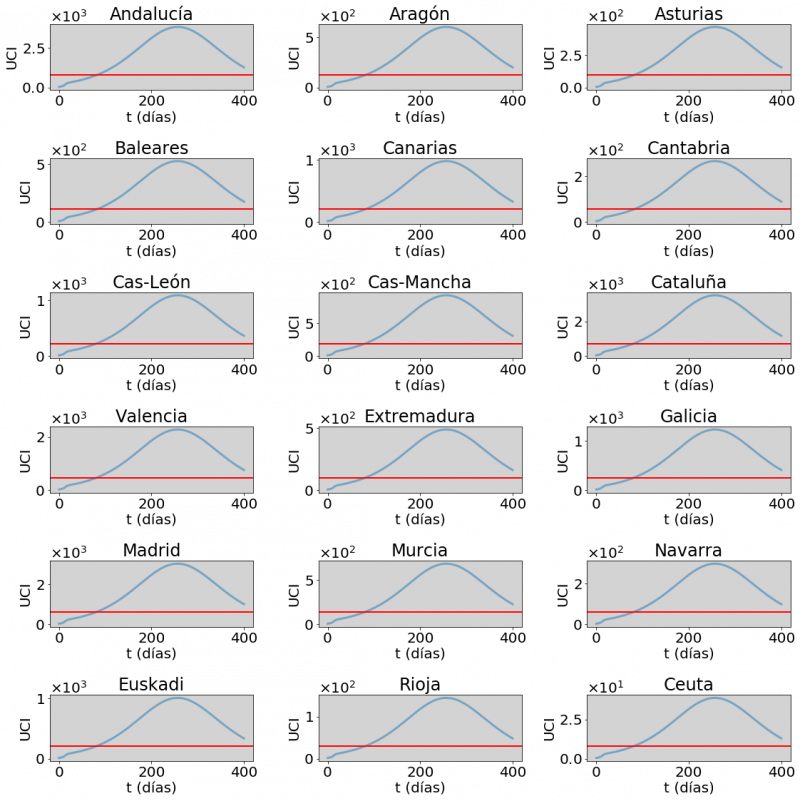
La figura 4 muestra tres variantes del escenario R que ya hemos descrito (es decir, las medidas se toman de golpe el 15 de marzo). Los paneles superior, central e inferior se corresponden a los casos en los que se consigue reducir R0 al 60 %, 40 % y 35 % de su valor. Las curvas azules se corresponden al número de enfermos que precisan ser ingresados en la UCI y que estimamos como 5 % de los infectados. La capacidad de cada comunidad autónoma (línea roja) la estimamos a partir del número total de camas disponibles en la UCI en España normalizado a la población de cada comunidad. Como puede verse reducir R0 por 60% no evita en absoluto el «colapso sanitario». Reducirlo al 40 % lo retrasa en un par de meses (lo que no es poco, ya que permitiría que otros factores, como la posible estacionalidad del virus entraran en juego). Pero reducirlo al 35 % «resuelve» el problema y esencialmente aplana la curva.
 |
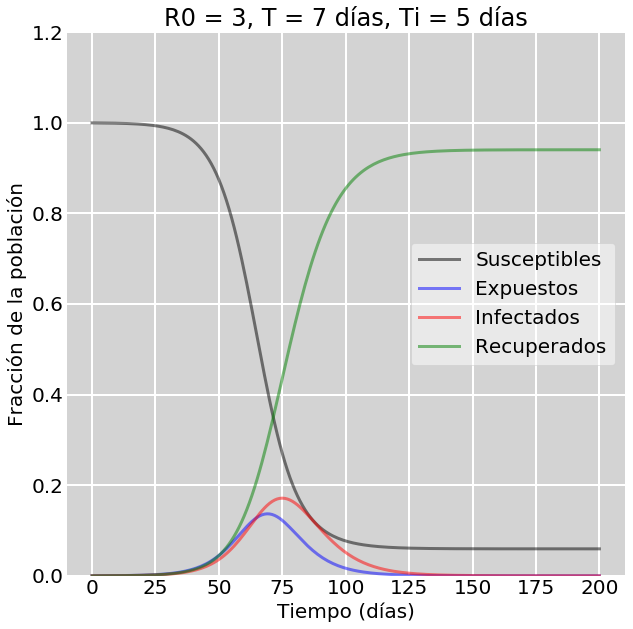 |
Figura 2: Panel izquierdo. Predicciones de SIR. derecho. Predicciones de SEIR.
Ahora bien, ¿en cuánto se traduce exactamente las actuales medidas de contención? Aquí se usa un modelo SEIR (más sofisticado que el que presento aquí, pero conceptualmente muy similar) en el que se estiman los factores de reducción debidos a las medidas tomadas en Wuhan y que varían entre reducir R0 al 65% de su valor en las etapas iniciales de la cuarentena (como hemos visto eso no sería suficiente) hasta reducirlo al 15% de su valor a partir del momento en que estas se endurecieron considerablemente. Probablemente las medidas que se han tomado en España y que son bastante duras estén en la zona intermedia, quizás 30-40 % de reducción. Si es el caso deberían ser bastante efectivas. Como mínimo retrasarían el colapso del sistema sanitario, lo cual daría tiempo a reaccionar si fuera necesario.
 |
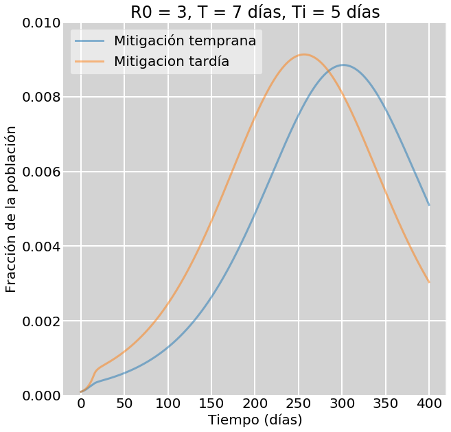 |
Figura 3: Escenarios de intervención temprana y tardía.
Es importante comprender que, si bien los científicos pueden ayudar mucho a manejar el excepcional problema que nos ha caído encima, la ciencia tiene también unos condicionantes que no podemos ignorar. Un estudio epidemiológico está basado en un modelo (que puede ser más o menos realista) y en un ajuste de datos que puede ser más o menos revelador (las cifras de casos declarados, por ejemplo, están aquejadas hoy en día de enormes incertidumbres, dada las fluctuaciones en los protocolos de realizar tests a los potenciales enfermos y la escasez de medios). En consecuencia, las conclusiones de un determinado estudio, aunque muy útiles —en cuanto aportan información valiosa elaborada por expertos—, deben tomarse cum grano salis. En condiciones «normales», el estudio en cuestión sería validado, desmentido, corregido o mejorado, mediante los mecanismos habituales del gremio. Los autores enviarían un artículo a una revista científica, seguiría un proceso de revisión de pares, eventualmente otros grupos realizarían análisis independientes, etcétera. Esto fue lo que ocurrió, por ejemplo, cuando los famosos neutrinos superlumínicos. La publicación del trabajo en el que se medía una velocidad de los neutrinos mayor que la de la luz causó un auténtico tsunami en la comunidad de físicos de partículas y en cuestión de meses se encontró el error en el análisis original. El problema hoy en día es que hay poco tiempo y esa premura nos puede llevar a saltarnos etapas. Y no hay que olvidar que las medidas que se están tomando y cualquier otra que se proponga tienen consecuencias serias para la economía, la salud, el bienestar y las vidas humanas. De ahí la necesidad de andar con tiento. Recordemos que el efecto de las medidas que se tomaron el 15 de marzo empezará a medirse en una o dos semanas más como máximo.
PULSAR EN LA IMAGEN PARA AMPLIAR
 |
 |
 |
Figura 4: Tres escenarios de mitigación. Los paneles superior, central e inferior se corresponden a los casos en que se consigue reducir R0 al 60 %, 40 % y 35 % de su valor antes de las medidas. Las curvas azules se corresponden al número de enfermos que precisan ser ingresados en la UCI. La línea roja marca la capacidad en la UCI de cada comunidad autónoma. Como puede verse, reducir R0 por 60% no evita en absoluto el «colapso sanitario». Reducirlo al 40 % lo retrasa en un par de meses (lo que no es poco, ya que permitiría que otros factores, como la posible estacionalidad del virus entraran en juego). Pero reducirlo al 35 % «resuelve» el problema y esencialmente aplana la curva.
De lo que no cabe duda es que nos espera todavía un largo periodo de confinamiento y disgustos exponenciales. Pero no puede llover para siempre. Estos tiempos de distancia, en los que no nos atrevemos a acercarnos a menos de dos metros del vecino, son también tiempos de cercanía y solidaridad. En palabras de Dickens, vivimos el mejor de los tiempos, el peor de los tiempos, la edad de la sabiduría, la edad de la estupidez, la época de creer, la época de no creer, la estación de la luz, la estación de la oscuridad, y, si se me permite darle la vuelta a la frase del genio, el invierno de la desesperación, la primavera de la esperanza.
(Pincha aquí para acceder al simulador de la evolución del Covid19).
[1] Backer JA, Klinkenberg D, Wallinga J. The incubation period of 2019-nCoV infections among travellers from Wuhan, China. medRxiv 2020; published online Jan 28. DOI:10.1101/2020.01.27.20018986









Antes de nada, un artículo genial. Pero me surge una duda:
En la figura 3 pones de ejemplo que en el escenario T se toman las medidas escalonadamente.
No sería más correcto para compararlo con el escenario R que en T las medidas se tomasen de golpe? Es decir, que se redujese R0 al 40% desde el día 1.
Muchas gracias por estos buenos artículos. Estaría muy bien si también pudieses analizar cuál fue la influencia de las manifestaciones del 8M en la evolución de la pandemia. A tenor de los datos aportados por el gobierno, no parece tan elevada, ya que:
1) el número de casos en Madrid no se ha disparado tan exponencialmente
2) todas las CCAA parecen tener una curva muy similar de evolución
Se agradecen esfuerzo, aportación y didáctica.
Interesaría conocer el impacto «real» en las curvas
del denominado Permiso Retribuido Recuperable.
Saludos y Salud.
También se agradecería saber qué otros factores pueden empinar la curva que llevaría al colapso del síndrome RALHP (Resistencia al Aburrimiento y Lamento por Horas Perdidas). Bromas aparte agradezco al autor de este artículo, componente de esa ínfima parte de la población mundial que se dedica a los oficios de los números con pasión, con la peculiaridad de que trabajan en el más absoluto silencio y soledad, solos, consigo mismo. Creo que cada vez tendremos mas necesidad de los científicos o, por lo menos, mayor presencia en todas las áreas del quehacer público.
Pingback: La evolución de la pandemia: ¿qué nos dicen los modelos? | Una vista circular
Yo no soy experta en este terreno, ni mucho menos, pero me surgen varias dudas.
Al menos en los países de nuestro entorno, se supone que todos los gobiernos se han apoyado en los consejos de expertos en epidemiología (entre otros), y sin embargo, las medidas tomadas han sido distintas en casi cada uno de ellos, y los resultados, aparentemente, también diferentes. De momento en GB, hasta hace solo unos días, no se habian tomado apenas medidas de mitigación, y no digamos en EEUU…
¿Eso quiere decir que parten de que el factor R0 es completamente diferente en cada país?, ¿eso significaría que la contagiosidad del virus no sería intrínseca al virus sino a factores externos?, tal y como se deduce al decir que España e Italia somos países con fuerte relación social y familiar. En esa situación hay otros países, como se está viendo, por ejemplo en la India, con una densidad de población tan elevada, sin medidas de protección ni confinamiento, ¿qué porcentaje de la población se prevé que se vería infectada y cuanta podría morir?
Por otro lado, en la catastrófica situación de la falta de ICUs para los casos graves, como se ha visto en España e Italia (también en China y eso que ya sabían como podía ser una epidemia de ese tipo), ¿eso llevaría a la muerte más o menos masiva de la población en riesgo de modo que al quedar poca población en riesgo el sistema sanitario se desahogaría y mayoritariamente, quedarían casos leves y manejables, y en consecuencia, se podría dejar el confinamiento?
Otro punto con el que no termino de estar de acuerdo, es el supuesto de que cuando llegue de nuevo la estación de estas infecciones (finales del otoño más o menos), incluso si hubieran desarrollado una vacuna, se plantean que podría haber mutado de nuevo a una cepa que no fuera neutralizada por la vacuna…., me parece que es augurar mucho (y no es que no pueda ocurrir), es decir, ¿Ésto no podría pasar cada año y no solo con los coronavirus?, los mismos virus de la gripe lo podían hacer cada año, y sin embargo no se montan estas pandemias con facilidad (por suerte, aunque habría que revisar el origen de ésta y como se podría haber evitado en origen), que ya había pasado antes…
Además, el paso de los virus de persona a persona, no tiene que derivar en cepas más patógenas, también cabe la posibilidad de que se atenúen y pasen a ser como los demás coronavirus estacionales del enfriamiento común
¡Gracias!