
El día 8 de marzo publicaba, junto con Carlos Pena, un artículo, «El coronavirus y la leyenda del tablero de ajedrez», cuyo principal objetivo era resaltar la necesidad urgente de medidas de contención. En esas fechas se celebraban todavía eventos que implicaban aglomeraciones masivas de personas, en concreto las manifestaciones del 8M que aglutinaron del orden de 220 000 participantes en Madrid y más de medio millón en toda España. Siete días después, la curva epidemiológica en España ha superado a la de Italia y el número de casos «oficiales» a la hora de escribir estas líneas se acerca a los 12 000. El número real de infecciones es, posiblemente, al menos un factor 3 más alto. Como consecuencia se ha declarado en España el estado de alerta, que impone una serie de medidas draconianas con el ánimo de frenar la expansión de la enfermedad. Los efectos de estas medidas van a tener un importante impacto en la economía y desde luego van a alterar sustancialmente nuestras vidas. Vale pues la pena preguntarnos qué beneficios podemos esperar del esfuerzo colectivo que la situación exige.
La semana pasada usábamos la metáfora del tablero de ajedrez para ilustrar como, en las fases iniciales, una epidemia se caracteriza por crecer exponencialmente. Recordemos la leyenda de sabio Sissa y el rey: un grano de trigo por la primera casilla, dos por la segunda, cuatro por la tercera y así sucesivamente, por cada casilla el doble de granos que por la anterior. En términos de una enfermedad infecciosa, la primera persona contagia a dos, esas dos a otras dos (por tanto 2 x 2 = 4 infectados), etc. El número de personas que cada persona infectada contagia en promedio se llama número de reproducción básica (R0). Un patógeno que se propagara siguiendo la regla del tablero de ajedrez tendría R0 = 2. En el caso de la terrible gripe española de 1918, R0 = 1.8. [1] La famosa gripe A de 2009 tenía R0 ~ 1.5 [1], mientras que para la gripe estacional R0 ~ 1.3 [1]. En el caso del COVID-19, los valores de R0 =2-4, con un valor medio del orden de 3 [2]. Es, decir, cada persona infectada contagia en promedio a otras 3 y por lo tanto la progresión de la exponencial (3, 9, 27, 81…) crece más rápido aún que la del tablero de ajedrez.
Otra diferencia importante entre apilar trigo en cada casilla del tablero y propagar una enfermedad infecciosa es que en el primer caso el número de granos de cereal está perfectamente determinado (1, 2, 4, 8, 16,…) mientras que el número de contagios en cada encuentro es una cantidad aleatoria, cuyo valor medio es R0. Eso quiere decir que cada historia individual puede variar considerablemente. Si nos fijamos en un individuo infectado concreto y contamos cuántos contagia a su vez, el número puede cambiar bastante, con una probabilidad nada despreciable de que sea cero pero también bastante considerable de ser diez o más. Lo mismo ocurre con la siguiente persona y así sucesivamente. Si promediamos las historias individuales, el valor que obtenemos es R0.
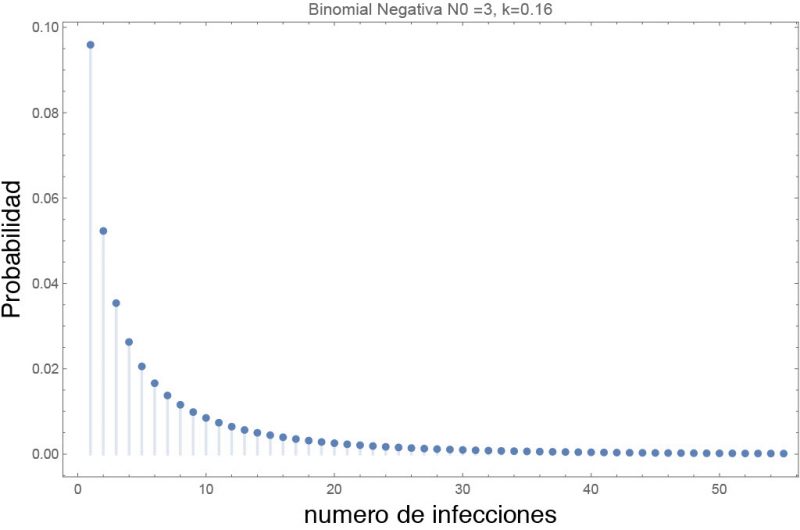
La figura 1 muestra la distribución estadística que se ha utilizado para describir R0. en epidemias similares a las del COVID-19, como la del virus del SARS en Singapur [3]. Se trata de la distribución binomial negativa, que depende no solo de R0 (cuyo valor en la figura es de 3) sino también de un parámetro llamado «parámetro de heterogeneidad», k (0.16 en la figura), que controla cuánta variabilidad puede haber entre el valor medio y los extremos. Como puede observarse, el resultado más probable es cero infecciones (con una probabilidad ligeramente inferior al 10 %). La probabilidad de un solo contagio es del orden de 5 %, la de dos un poco menos de 4% y la de tres alrededor del 3 %. Por otra parte, las colas son muy largas, lo que quiere decir que existe una probabilidad sustancial (del orden del 1 %) de contagiar de golpe a 20 o más personas. La binomial negativa permite incluir los llamamos eventos de supercontagio (super spreading events, o SSE), en los que un solo individuo puede infectar a decenas de personas y disparar un brote epidémico.
En consecuencia, no hay dos brotes idénticos. Para visualizar bien este efecto, imaginemos que un solo individuo infectado y en fase contagiosa se mueve libremente por una gran ciudad como Madrid. Imaginemos que vive solo y cada día sale de casa durante un cierto tiempo, digamos un par de horas. Va a la panadería, compra el periódico, quizás se toma un café en un bar o juega un rato al dominó en el casino. Supongamos que el lunes tose a corta distancia del panadero, el martes disfruta de un vermut con los amigos (todas las manos van al mismo plato de frutos secos) y el miércoles acude a una manifestación y comparte pancarta con veinte camaradas. Un posible resultado de estas acciones es que el lunes infecte al panadero, el martes no infecte a nadie y el miércoles contagie a diez de sus compañeros. Estamos iniciando tres brotes potenciales. La propagación del brote del lunes va a depender de lo que haga el panadero (presumiblemente, dado su trabajo, lo va a transmitir a otros, pero quizás este panadero es muy tímido y no se acerca a nadie). El brote del martes ni siquiera llega a producirse. En cambio, el miércoles hemos iniciado un SSE y ahora cada uno de los diez infectados puede a su vez, propagar el virus.
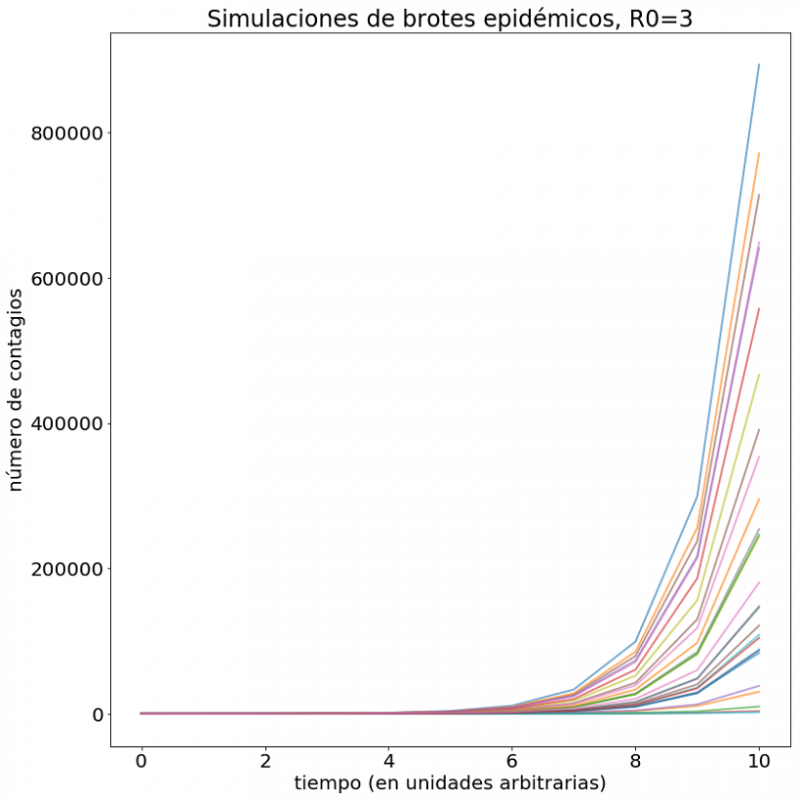
La figura 2 muestra una simulación de esta situación. Partiendo de un solo individuo, lanzamos 100 posibles brotes (que se corresponderían a los paseos por Madrid de nuestro sujeto, digamos que a lo largo de 3 meses). Para simular la evolución del brote procedemos de la siguiente forma. Empezamos por lanzar un número aleatorio de acuerdo a la binomial negativa de la figura 1 (por tanto obtendremos 0 un 10 % de las veces, 1 un 5% y así sucesivamente). Si el resultado es 0, el brote no cuaja. Si el resultado es distinto de 0 pasamos «a la siguiente casilla» de la infección. Imaginemos que el resultado de arrojar el dado es 1. En el siguiente paso, lanzamos otro dado siguiendo la binomial negativa y obtenemos 2. A continuación lanzamos 2 dados, uno por cada nuevo caso del paso anterior. Supongamos que el primero nos da 3 pero el segundo nos da cero, tenemos por tanto 3 casos y pasar a la siguiente casilla implica arrojar 3 nuevos dados. Supongamos que dos de ellos dan cero y el tercero da uno, tenemos entonces 1 nuevo infectado. Finalmente arrojamos un dado y el resultado es 0. La historia de este brote sería (1,2,3,1,0) y no prosperaría. De hecho, el 75 % de las simulaciones resultan en brotes abortados. Pero en un 25 % de los casos, la infección se dispara. La figura 2 muestra la progresión de estos últimos casos en 10 pasos o unidades temporales. Algunos no prosperan mucho, pero otros crecen endemoniadamente, llegando al millón de contagios. Cada unidad temporal se corresponde a un cierto número de días relacionado con el periodo en el que los individuos son infecciosos, pero por ahora no necesitamos preocuparnos de su valor concreto. El mensaje es este: debido a la naturaleza aleatoria del proceso de contagio, la mayoría de los brotes potenciales abortan por sí solos. Sin embargo, unos pocos prosperan y de estos, unos pocos pueden crecer más rápidamente que el trigo del sabio Sissa. Cuando un patógeno presenta un número reproductivo tan alto, basta un solo individuo para disparar una pandemia.
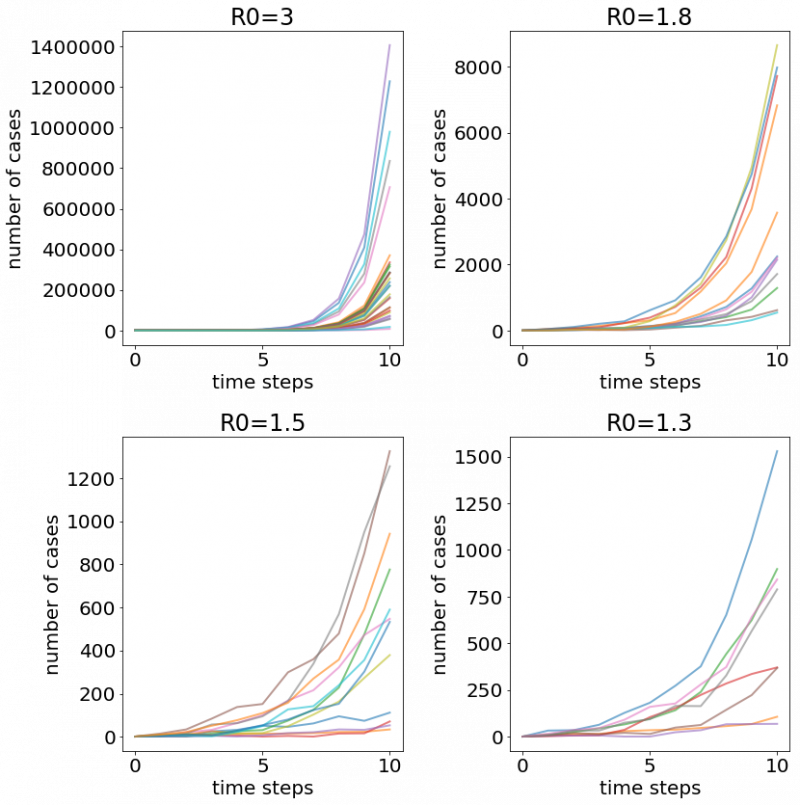
La figura 3 compara la evolución de el COVID-19 (R0 =3), con la gripe española (R0 =1.8), la gripe A (R0 = 1.5) y la gripe común (R0 =1.3). Cada línea en los gráficos se corresponde a una epidemia, originada por una sola persona, tal como acabamos de describir [4]. Para cada uno de los casos se iniciaron 100 simulaciones, de las cuales 25 se dispararon exponencialmente para COVID-19, 12 para la gripe española y la gripe A y 8 para la gripe común. En otras palabras, la «tasa de éxito reproductivo» para COVID-19 es el doble que para la gripe española y el triple que para la gripe común.
Además, si examinamos el número de infecciones de COVID-19 al cabo de 10 unidades temporales en la epidemia con más éxito (esto es, la que produce el mayor número de casos) vemos que esta alcanza el millón y medio de contagios, a comparar con unos 8000 para el caso de la gripe española y del orden de 1500 para las otras dos gripes. En otras palabras, si atendemos solo al valor de R0 (hay otros factores a tener en cuenta y que comentaremos más adelante), COVID-19 (con R0=3), produce, en el mismo tiempo, diez veces más infecciones que la gripe común o la gripe A.
¿Cómo controlar una epidemia? La respuesta de cajón es reduciendo el valor de R0. Esto es posible ya que dicho valor depende fuertemente del patógeno, pero también de otras variables entre las que se incluye el nivel de contacto social de la población. Por muy infeccioso que sea un virus, si las personas infectadas no están en contacto con nadie es imposible que se trasmita, es decir, R0 sería nulo en este caso. Por tanto, el valor de R0 se puede modificar con medidas de aislamiento. De hecho, incluso si no se toma ninguna medida, llega un momento en que la mayor parte de la población ha sido infectada. En consecuencia el virus no encuentra nuevos huéspedes y R0 se reduce.
Precisamente esa parece ser la lógica del razonamiento de Boris Johnson (o sus asesores) para proponer una estrategia en la que no se toman medidas de aislamiento severas. Por otra parte, en ausencia de dichas medidas podría llegar a infectarse cerca del 60 % de la población del COVID-19. Por comparación, en el caso de la gripe común, la fracción máxima es del orden de 15-25 %.
La ventaja de permitir que la enfermedad prospere a sus anchas es que evita medidas tan drásticas como las que estamos sufriendo. Si la fracción de casos graves (y la fracción de fatalidades) fuera lo bastante pequeña, se trataría de una opción viable. El ejemplo más obvio es el resfriado común al que apenas prestamos atención. En el caso de la gripe A, durante el periodo comprendido entre el 12 de abril de 2009 y el 10 de abril de 2010, se registraron en Estados Unidos 60.8 millones de casos, 274 304 ingresos en hospital y 12 469 muertes [5]. El porcentaje de hospitalizaciones fue por tanto de 0.45 % y el de defunciones 0.02 %. Se trata de números mucho más pequeños que los del COVID-19, donde la fracción de casos graves es del 10-15 % y el número de defunciones puede situarse entorno al 1% (aunque el número aparente en España y otros países es bastante más grande porque no están contabilizados muchos casos positivos leves). Si consideramos que la fracción de la población que se infectaría del COVID-19 es mucho mayor que la correspondiente para la gripe A o estacional y si añadimos que el porcentaje de hospitalizaciones que requieren cuidado intensivo es alto y rematamos con el alto porcentaje de fatalidades (en el hipotético caso de que el 50 % de la población española se infectara el número de víctimas podría ser del orden de 200 000 asumiendo un 1% de tasa de mortalidad), la conclusión está bastante clara. El coronavirus no da otra opción que combatirlo activamente. No son pocos los científicos que están criticando las decisiones del gobierno de Johnson, aunque hasta el momento han tenido el mismo escaso éxito que aquellos que reclamaban medidas más urgentes y decididas en España hace unas pocas semanas.
Si decidimos actuar…¿cómo se combate esta pandemia? Una opción habría sido reaccionar inmediatamente, intentando abortar la exponencial antes de que se desbocara. Así ha sucedido en Corea, donde la combinación de una ciudadanía muy concienciada y el despliegue de una amplia batería de medidas preventivas, que han ido desde realizar pruebas de contagio masivas hasta el seguimiento exhaustivo de infectados, ha permitido controlar el virus hasta el punto de que el valor de R0 en ese país se aproxima ya a cero. Esa opción ya no es posible en España —donde las medidas de prevención no han alcanzado ni siquiera para disponer de un stock de mascarillas para uso de la población— y la única alternativa consiste en impedir la propagación del virus por las bravas, esto es, confinando a la población. Se trata de una medida brutal y con repercusiones económicas y sociales que todavía no sabemos apreciar bien, pero no van a ser baladíes. Por otra parte, es lo único que puede hacerse en este momento.
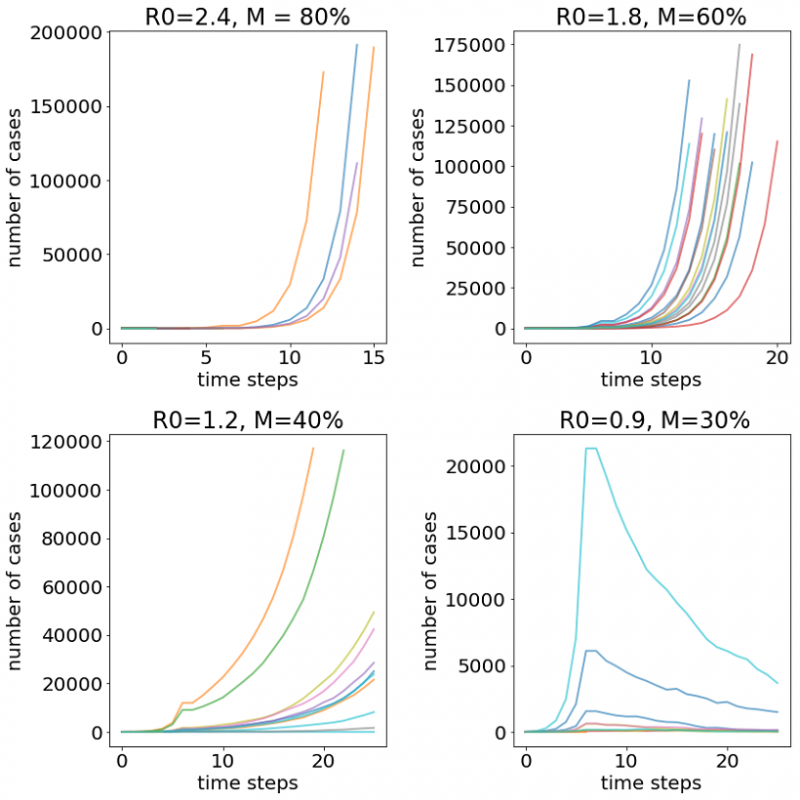
La figura 4 muestra cuatro escenarios, asumiendo un valor inicial R0 =3 (la situación actual en España). En los cuatro paneles se muestran simulaciones de brotes epidémicos, en los que, tras una fase inicial de crecimiento, se activan medidas que lo reducen por un factor (que llamamos factor de mitigación, M) del 80 %, 60 %, 40 % y 30 %, esto es, pasamos, después de tomar medidas a valores de R0 = 2.4, 1.8, 1.2 y 0.9. Como puede observarse, los brotes solo consiguen controlarse en este último caso.
Reducir R0 al 30 % de su valor actual no es fácil. La «receta de Wuhan» propugna confinar a los ciudadanos y en la práctica supone detener el país excepto en lo esencial para garantizar mínimos (abastecimiento, hospitales, etc.). La experiencia China indica que la fórmula puede funcionar, pero es claro que los costes pueden ser terribles.
¿Cuándo veremos resultados? ¿Cuánto tiempo tendremos que continuar encerrados? ¿Puede rebrotar la epidemia una vez que se relajen las medidas? ¿Hay otras medidas posibles, menos brutales que podrían haberse tomado o podrían tomarse en el futuro? Se trata de preguntas vitalmente importantes. Incluso si la actual situación puede revertirse en unos meses, es esencial que entendamos cómo seguir funcionando a partir de ese momento y no parece muy prudente poner todos nuestros huevos en la cesta de la posible naturaleza estacional del virus o la disponibilidad de una vacuna. Incluso si la incidencia de COVID-19 baja durante los meses de verano, presumiblemente volverá en otoño e incluso la población inmunizada por haber sufrido la enfermedad en esta oleada podrían volver a recaer si el virus muta. En cuanto a la vacuna, las estimaciones más realistas largo nos la fían. Por otra parte, para entender con detalle las posibles acciones en la guerra contra la pandemia (una guerra, que por el momento no vamos ganando), hace falta fijarse en otros parámetros fundamentales de las enfermedades infecciosas, como el tiempo de incubación, el periodo de contagio y la proporción de casos que no presentan síntomas y que comentaremos en la próxima entrega.
*Nota: El autor es físico de partículas y su campo de investigación es la física de neutrinos. Las técnicas matemáticas, estadísticas y de análisis de datos utilizadas por los físicos y los epidemiólogos tienen mucho en común, lo que me permite hacer uso de estas para elaborar modelos sencillos con propósitos divulgativos. El objetivo de esta serie de artículos es tratar de exponer de la manera más rigurosa y pedagógica que pueda unas cuestiones de importancia vital para todos, desde las obvias limitaciones que debe asumir quien no es un experto en la materia. Con todo, en palabras de mi abuelo, un grano no hace granero, pero ayuda al compañero. Mi agradecimiento a Pilar Hernández, por su aguda y crítica lectura de este trabajo.
(Continúa aquí)
[2] Temporal variation in transmission during the COVID-19 outbreak
[3] Lloyd-Smith et al, Vol 438|17 November 2005 | doi:10.1038/nature04153
[4] En todas estas simulaciones el contagio ocurre de manera inmediata y la persona contagiada infecta a tantos otros como corresponde a «lanzar el dado» de la binomial negativa. Se trata de una simplificación, pero nos sirve para hacernos a la idea de la virulencia de la enfermedad.
[5] Clinical Infectious Diseases, Volume 52, Issue suppl_1, January 2011, Pages S75–S82, doi.org/10.1093/cid/ciq012










Si tal y como se dice al final hay una componente aleatoria que puede hacer que con uno o unos pocos casos tengamos miles de contagiados ¿qué sentido tiene un confinamiento generalizado?
¿Por debajo de que cifra mínima se podrá salir de dicho confinamiento?
Esto nos conduciría por prudencia a muchos meses. No creo que la sociedad esté dispuesta a ello.
¿No es más razonable solo confinar al grupo de riesgo? ¿Y que el resto lo pase?
Le seguiremos en este viaje, aunque a veces me pierda entre tanto número y tanta fórmula.
Hola,
Alemania a día de hoy 28.796 infectados y 111 muertos. Lo que supone una tasa de mortalidad de 0,38 % de los infectados. Eso sin contar que habrá bastantes casos sin registrar.
¿Podría actualizar los modelos para el caso de Alemania y extraer conclusiones de estos? Quizá se esté introduciendo un cierto sesgo.
Gracias,
Buenos días,
La estructura social está marcando una diferencia más que clara en la evolución del virus, simplemente basta con fijarnos y comparar Italia y Alemania (caso opuestos).
Alemania a 24/03/2020.
32.024 positivos 143 muertos.
Italia a 24/03/2020.
63.927 positivos 6.077 muertos.
A años luz el uno del otro, pero claro para sacar modelos, binomiales, simulaciones necesitamos un numerador y un denominador, y no lo tenemos ¿Qué pasaría si realmente en Italia se han contagiado 1.000.000 italianos y la gran mayoría asintomáticos? Significaría un número enorme de personas inmunes ahora mismo y no tendría nada que ver con lo que se refleja en este artículo ni en el siguiente.
De igual forma si en Alemania hay (imaginemos) 60.000 infectados, de los cuales solamente tenemos noticia de 32.024 casos con 143 muertos, podríamos decir que para el caso de Alemania y para su estructura social, las medidas tan restrictivas tomadas a día de hoy en España no aplican, para ellos es como una gripe (suave).
Lo mismo en el caso de que el virus sea estacional, etc, etc.
El comentario anterior iba en la misma dirección y lo mismo el primer comentario del artículo acerca de una estratificación de quienes pueden y quienes no pueden salir o hacer vida normal.
Buenos días,
No entiendo porqué se utiliza la binomial negativa para los contagios. La Binomial Negativa se define como el número de experimentos (o de fracasos) hasta conseguir k éxitos (entiendo que en este caso contagios). No llego a ver cuáles son todos los parámetros. He buscado información sobre esta distribución como modelo para contagios y no la encuentro.
¿Sería tan amable de explicarlo más ampliamente o adjuntar algún enlace con información al respecto?
Muchas gracias,
Hola,
Muchas gracias por la serie de artículos.
Parece que hay un error en la figura 1 (o en el texto que lo acompaña). El casi 10% corresponde a 1 contagio (y no cero), el 5% a 2 contagios (y no 1), y así sucesivamente. Y en el gráfico no aparece nada relacionado con 0 contagios.
Espero que no modifique toda la teoría ?
Un saludo,
Pingback: La evolución de la pandemia: ¿qué nos dicen los modelos? | Una vista circular
¡Gracias!
Qué pensarías si un epidemiólogo escribiese un artículo de «divulgación» sobre la oscilación de neutrinos y los aportes de Bruno Pontecorvo? Tú dirías que dado que no es un físico de partículas no tiene la formación para escribir un artículo en ese tema? Entonces, siendo tú un físico de partículas cómo te atreves a escribir un artículo de «divulgación» sobre las epidemias si no eres epidemiólogo? Es como si dijeras que puedes hacer una operación a corazón abierto sin ser médico. La Epidemiología merece respeto. Tu intención puede ser buena pero estás generando confusión entre la gente que no sabe nada de Epidemiología. Haces pensar que un matemático o un físico puede remplazar a un epidemiólogo y eso es totalmente falso. Tu no sabes nada del trabajo de campo en Epidemiología y asumes una actitud pedante y megalómana. Dedícate a lo tuyo y dejo que los epidemiólogos hagan su trabajo.