Clara Grima: Los colores de la radio

Puede parecernos mentira, pero es verdad: los que deambulamos por lo que se ha dado en llamar el mundo 2.0 tenemos una visión reducida de la realidad del mundo real. Sí, pudiera parecer que el hecho de poder opinar en las redes sociales y en los blogs de manera libre y sin censura nos permite llegar a todos los rincones de este, nuestro amado país. Pero nada más lejos de la realidad, me temo. No hay más que ver la cara que me ponen en la peluquería de mi pueblo cuando alguien dice algo con lo que estoy de acuerdo y yo digo con el pulgar hacia arriba: «retuit».

Tonterías aparte, existen muchos ejemplos de que, hoy en día, a pesar de todos estos medios en los que los ciudadanos se expresan libremente, el control de los medios de comunicación tradicionales (televisión, radio y prensa escrita, en orden decreciente de importancia) es fundamental para moldear la opinión pública.

Fíjense, si no, en la de años que Berlusconi ha conseguido estar en el poder o muy cerca de él a pesar de todo lo que sabíamos sobre él: en Italia, la mayoría de los ciudadanos lo que recibían eran las noticias de una prensa de la que es el dueño. O, sin movernos de nuestro suelo patrio: muchos se han extrañado de que en las últimas encuestas el partido que más ha subido sea el PP, a pesar de la crisis, de los Bárcenas, de los Werts y de los relaxing cups. En nuestro país, la derecha tiene muy claro que hay que controlar los medios de comunicación y hacer todo lo posible para que los no afines se consoliden (con ayudas económicas institucionales desproporcionadas a la tirada de los medios, por ejemplo, como la campaña de Sanidad en la que favoreció a La Razón y otros medios similares) o comprando las cadenas de televisión que no les eran cercanas (Cuatro y La Sexta). Miedito da que el señor Lara diga que quiere que La Sexta, su televisión, sea «una televisión de centroizquierda, seria y respetuosa con la derecha ya que no lo es todavía», y que don José Manuel diga, además, de Marhuenda que es un gran profesional. Ay.

Pero ese control de los medios de comunicación se extiende mucho más allá y podemos comprobar cómo los gobiernos de derecha se caracterizan por favorecer de forma descarada a los medios afines a la hora del reparto de frecuencias tanto en las radios como en las TDT locales. Lo que ocurre es que este tipo de noticia suele pasar desapercibida (la SER o algún otro medio protesta un poco, pero como nadie comparte su malestar, pronto se acallan dichas voces discrepantes). Que quede claro que no digo que la SER no sea la radio más escuchada en España, lo que digo es que desde instancias oficiales, cuando se trata de repartir frecuencias en sitios concretos, se favorece siempre a los medios de la derecha. Algunos ejemplos son las siguientes noticias: esta o esta.

Para ser ecuánimes, a veces la derecha también protesta del reparto de gobiernos de la izquierda.

Puede que más de uno se pregunte: ¿por qué hay que repartir las frecuencias? ¿Por qué cada cual no pone su emisora de radio donde quiera y emite sin más? ¿Por qué otorgar ese poder a los políticos como si no tuvieran ya suficiente? Por las interferencias, claro.

Pues por sorprendente que parezca, la física y las matemáticas juegan un papel fundamental en esta historia. Cómo me gustan los maridajes entre física y matemáticas… (suspiro)

El rol de la física es sencillo de vislumbrar: estamos hablando de emisión de ondas y por tanto de interferencias. Así que voy a tratar de explicar por qué hemos de tener en cuenta también a las matemáticas.

Es fácil deducir que si dos emisoras cercanas emiten en una frecuencia también cercana, se puede producir una interferencia entre ellas; por lo tanto, habría que evitar la asignación de frecuencias semejantes a emisoras que no disten mucho entre sí y no disponemos de un número infinito de frecuencias para hacerlo. Entonces, ¿cómo se puede resolver este problema?

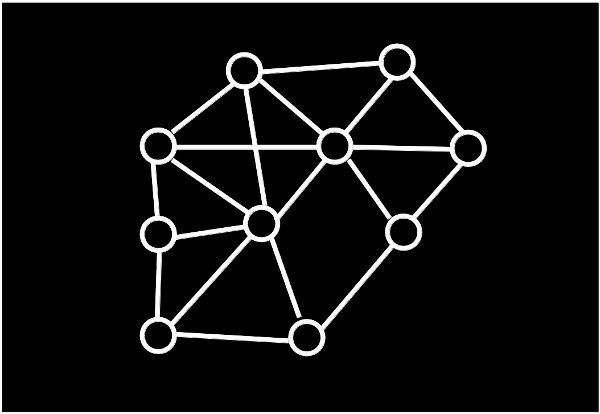
Supongamos que el siguiente gráfico muestra una determinada zona geográfica y que cada puntito (o circulito) señala la ubicación de nuevas emisoras de radio. Hemos unido con una línea, de dos en dos, a aquellas emisoras para las que, por la geografía, pudieran existir interferencias entre ellas si se les asignan frecuencias cercanas.

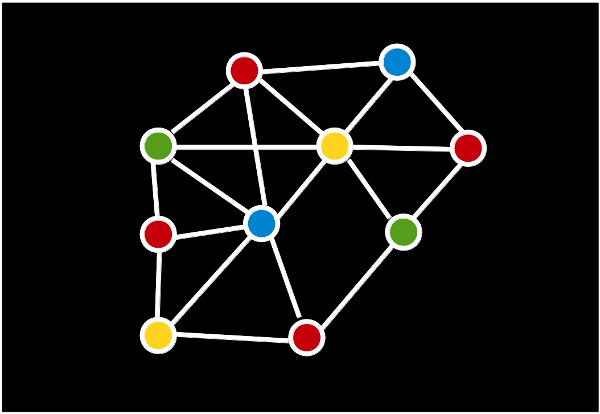
A continuación, vamos a colorear (espero que no me riñan los jefes de Jot Down por bombardear la estética de la revista) los circulitos, a los que a partir de aquí llamaremos vértices, de forma que dos vértices que estén unidos por una línea, a las que llamaremos aristas, no tengan el mismo color.

Ea, pues ya está. Cada color representa una frecuencia y han bastado con cuatro (hemos usado cuatro colores) para resolver el problema en esta zona geográfica. Lo que estamos haciendo es representar el problema con un grafo, con vértices y aristas, y dar una coloración de vértices para el mismo.

Es este, el problema de coloración de vértices de un grafo (sin que dos vértices unidos por una arista tengan el mismo color) uno de los problemas más difíciles de resolver en Teoría de Grafos: el decidir cuál es el menor número de colores necesarios para colorear los vértices con esa condición. Además de la asignación de frecuencias a emisoras de radio, tiene infinidad de aplicaciones en problemas de optimización, minimización, de recursos. Sin duda, una de las aplicaciones más fáciles de entender es la de la distribución de invitados en las mesas de un banquete de boda.

Que sí, hombre. Hay que repartir a los invitados en mesas, hay un número concreto de estas, y hay que tener cuidado de no sentar juntas en la misma mesa a tu tía Adela con tu tía Emilia, que no se hablan; o a tu cuñado Juan con tu primo José que se pelearon por los encantos de Lola… En fin, que, normalmente, hay incompatibilidades humanas y se hace necesaria una buena planificación de las mesas para que aquello no acabe en arañazos y/o en camisas rotas, si no hay necesidad de ello. Se trata simplemente de asignar un vértice a cada invitado conflictivo, unir con una arista a las parejas incompatibles para compartir mesa y colorear el grafo como hemos dicho: sin que vértices unidos entre sí tengan asignado el mismo color. Eso sí, procura necesitar un número de colores menor o igual que el número de mesas del banquete… No siempre es posible.

Como he dicho unas líneas arribas, el problema de la coloración de vértices de un grafo con el mínimo de colores posibles es un problema muy difícil, NP-duro le decimos los matemáticos, vamos, que no se puede diseñar un programa (para el ordenador) que lo resuelva en todos los casos. Pero si el grafo es plano, es decir, se puede dibujar sin que se crucen las aristas, se sabe que, como máximo, se necesitan cuatro colores. Este resultado es bastante conocido, es el Teorema de los cuatro colores.

Por otra parte, a los vértices que tienen el mismo color en una coloración, se les llama independientes, porque no existe relación entre ellos. Y eso nos lleva a otro problema de los difíciles de la Teoría de Grafos: encontrar el conjunto de vértices independiente más grande (con más elementos) dentro del grafo. Sí, otro de esos NP-duros. Pero resulta muy interesante encontrar conjuntos de emisoras (vértices) independientes porque a todos ellos les bastaría con una misma frecuencia sin miedo a interferencias.

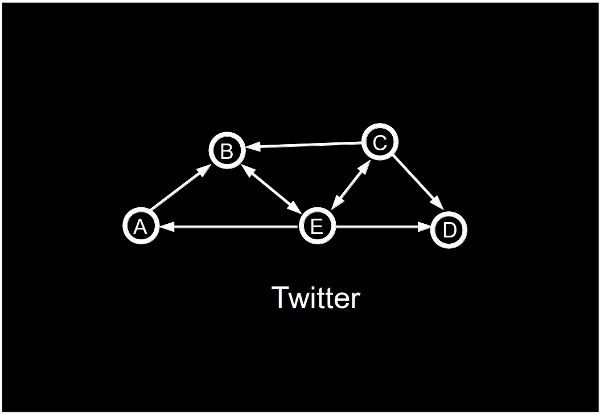
Pero en el tema de las emisoras también resulta interesante que estas lleguen a cuanta más gente mejor. Vamos a hablar ahora de otro concepto, a mi juicio, interesante en el tema de la transmisión de información. Lo vamos a ver con redes sociales, que puede ser más asequible. Si pensamos en Facebook, la representación de esta red se hace con un grafo en el que los usuarios serían los vértices (los puntitos) y si dos usuarios son amigos en la red, los unimos con aristas. Pero si pensamos en Twitter, nuestras aristas deben indicar además una dirección, puesto que el hecho de que tú sigas a alguien en Twitter no implica que ese alguien te siga a ti. A estos grafos, a los que tienen dirección en las aristas, les llamamos grafos dirigidos o, para simplificar, digrafos. En la figura siguiente, representamos, entre otras cosas, que A sigue a B pero B no sigue a A, que B y E se siguen mutuamente, etc.

Pues bien, si se quiere controlar la información que llega a todos los usuarios de la red, o a todos los oyentes de las emisoras (para el ejemplo de las emisoras, podemos una flecha de cada oyente a la radio que suele sintonizar) lo ideal es conseguir un conjunto de vértices absorbente, es decir, un conjunto de vértices de forma que cualquier elemento del universo a informar y/o controlar siga a alguno de ellos.

En la figura anterior, el conjunto formado por B y D es un conjunto absorbente: cualquier otro usuario de la red «escucha» lo que digan ellos. O sea, que controlando lo que digan B y D, tenemos controlado lo que escuchan el resto de usuarios. Al contrario que con el problema de conseguir conjuntos independientes, que los queremos cuanto más grandes mejor, en el caso de conjuntos absorbentes lo que interesa es que sean lo más pequeños (con menos elementos) posible. ¿Por qué? Pues porque necesitaremos controlar a menos elementos para controlar a toda la población.

Uniendo los dos conceptos anteriores, lo que interesaría para una «buena» manipulación de la información en radio o en Twitter, por ejemplo, es conseguir un conjunto de emisoras independiente (no se pisan) y absorbente (llegan a todo el mundo). En Teoría de Grafos, si se consigue un conjunto de vértices así, independiente y absorbente, se le llama núcleo del grafo. Ojo, no todos los grafos tienen que tener núcleo.

Pero como a mí no me mola el uso del núcleo de un grafo para controlar la información al pueblo, ni mucho menos, les voy a contar una aplicación de todo esto más lúdico y festiva: una estrategia ganadora para un juego simple que proponer a algún colega a la hora del café.

El juego, para dos jugadores, consiste en lo siguiente: por turno, cada jugador dirá un número natural del 1 al 3, es decir, 1, 2, o 3. Se van sumando y gana el primero que llegue exactamente a 31. Pueden apostar quién pagará le café esa mañana, por ejemplo. Ahora bien, si el primer jugador conoce el núcleo del grafo asociado al juego, ya puede ir sacando el monedero el segundo…

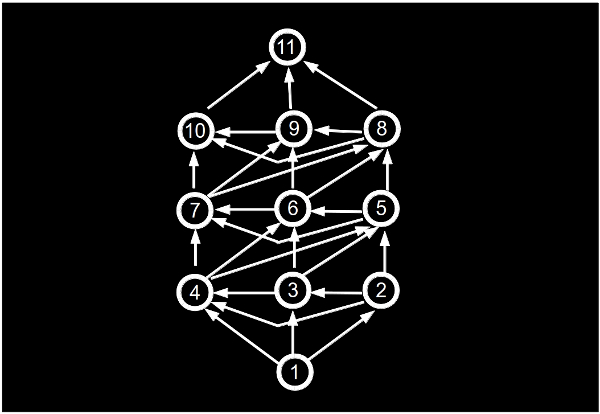
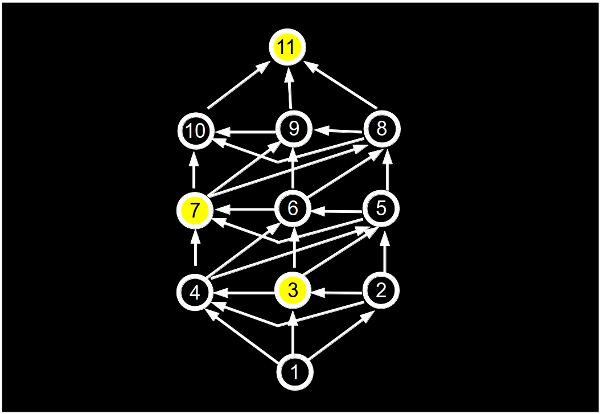
¿Cómo? Lo voy a tratar de explicar pero llegando a 11 en lugar de a 31, por una razón muy sencilla: el razonamiento es idéntico y el dibujo de grafo sale más simple. Dibujamos el siguiente grafo con 11 vértices, dibujando una arista dirigida (con flecha) desde un vértice a otro si se puede llegar del primero al segundo sumando 1, 2 o 3. Por ejemplo, de 7 a 10, ya que 7 más 3 es 10 y puedo llegar.

Ahora se trata de construir un núcleo para este grafo que contenga al 11, que es el objetivo. Les recuerdo que el núcleo es un conjunto de vértices independiente (no hay aristas entre los elementos del núcleo) y absorbente (cualquier vértice del grafo está conectado con alguno del núcleo). Si cogemos al 11 como primer elemento del núcleo, el siguiente vértice (en orden decreciente) que podremos elegir para dicho núcleo será el 7, ya que tanto el 8, como el 9 y el 10 están conectados al 11 y queremos un conjunto independiente. Elegidos el 11 y el 7 para nuestro núcleo, el siguiente tiene que ser el 3 que es el primero que encontramos que no se conecta a ninguno de estos dos. Y fin. Ya no podemos elegir más vértices y que siga siendo un conjunto independiente. Falta comprobar que este conjunto, el formado por 3, 7 y 11 es absorbente. Pero si se fijan en la ilustración, verán que cualquier otro vértice del grafo está conectado (sigue, en el argot de Twitter) a alguno de ellos, como si fueran el conjunto de guruses de Twitter, por ejemplo.

Pues ya lo tienen. Si empiezan diciendo el 3, ya han ganado. Diga lo que diga su adversario, ustedes dicen el número que sea necesario para llegar a 7, le dejan hablar y luego completan hasta 11. No hay forma de perder. Una vez que usted ha «entrado» en el núcleo, su adversario no puede entrar. Una vez dentro del núcleo, para ganarse el café solamente debe seguir las baldosas amarillas, que en este caso son los elementos del núcleo. Y ganar. Para el juego con 31, el núcleo sería {3, 7, 11, 15, 19, 23, 27, 31}.

Espero que les sepa bien el café ganado y que me inviten a uno si el juego les gustó y nos cruzamos en alguna cafetería.

También espero no arrepentirme de haber sugerido estrategias de control de la información a nadie, aunque me temo, porque llevo las orejas puestas cuando salgo a la calle, que ellos ya lo hacen muy bien sin usar ni Teoría de Grafos ni leches. Algunos hasta ofreciendo una barra de pan en un país en el que mucha gente está pasando hambre…

Pero qué… pic.twitter.com/YiYr5jsenJ

— Jot Down Magazine (@JotDownSpain) October 10, 2013

Recuerda a aquello que hacen en Grecia los de Amanecer Dorado y que tan alegremente heredaron algunos paisanos nuestros de Valencia. Sin acritud.